페르미-디랙 분포(Fermi-Dirac distribution)는 임의의 온도 T에서 에너지 준위 E가 입자에 의해 채워질 확률을 나타낸다. ==> 무슨 말인가? 아무리 전공서적을 봐도 몰랐지만 이제는 알겠다.
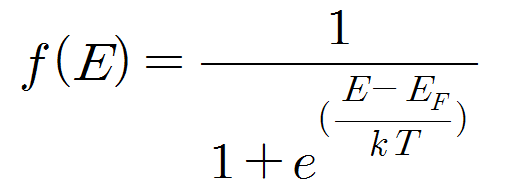
f(E)=E 라는 에너지를 지닌 '전자'가 존재할 확률
k=볼츠만 상수
T=절대 온도
Ef=페르미 레벨 or 페르미 준위
그냥 직접 숫자를 대입해보자
1) E=Ef일 때
f(E)=1/2
즉, 50% 확률로 전자가 존재한다는 뜻이다 ==> 전자의 50%가 존재한다는 뜻은 아니다.
==> 페르미 레벨의 전자가 존재할 확률은 50%이다. 이것은 온도에 영향 받지 않는다.
2) T=0 (절대온도), Ef=!0일 때(0이 아닐 때)
f(E)=1 (E가 Ef보다 작을 때)
f(E)=0 (E가 Ef보다 클 때)
즉, 절대온도 0도에서 페르미 준위보다 낮은 전자는 100% 존재하고
높은 레벨의 전자는 존재할 수 없다는 뜻

온도가 높아지면 이 분포함수는 완만해진다

간단하게 생각하면
온도가 높아지면서 페르미 레벨보다 높은 준위의 에너지를 갖을 수 있게 되는것이다.
정리

페르미 준위= 절대온도 0도일때 가질 수 있는 최대의 에너지 상태.
즉 0도에서 최외각 전자가 갖는 에너지 상태.
그렇기 때문에 0도에서 페르미 에너지보다 높은 에너지 준위를 갖는 전자가 존재할 확률은 0이고
그보다 낮은 전자가 존재할 확률은 100%이다.
온도가 높아짐에 따라 페르미 분포함수는 완만해진다.
'반도체 이야기' 카테고리의 다른 글
| [MOSFET 구동원리] 간단하게 설명하기 (0) | 2022.01.24 |
|---|---|
| [PN 접합] 간단하게 설명하기 (0) | 2022.01.24 |
| 반도체 8대 공정 [1-5] (0) | 2021.02.21 |
| 반도체 8대 공정 [1-4] (0) | 2021.02.18 |
| 반도체 8대 공정 [1-3] (0) | 2021.02.17 |