
1. 벡터, 좌표값
오늘은
벡터 좌표계 좌표값 그리고 좌표변환행렬에 대해서 알아보도록 하겠습니다.
벡터라고 지칭한것은 수치의 묶음이다.
어떤 수치들의 집합을 표현한것을 벡터라고 했습니다.
앞으로 3차원 운동을 표현하기 위해
세밀하게 표현해보죠
단순하게 화살표로 이해하면 좋을것 같습니다.
시작점이있고 끝점을 표현하는것이죠.
벡터의 좌표값은 수치들을 표현하기 위해서는
좌표계가 필요한데요. 세개의 단위벡터들이 서로 직교하게 형성이 된 경우에 좌표계가 정의된다.
좌표값은 네개의 절차를 가지고 형성을 할 수 있다.
i) 각 기저벡터 방향으로 선을 무한대로 연장하고
ii) 각 기저벡터의 길이만큼의 간격으로 각 연장선에 눈금을 표시한 후
iii) 임의 벡터의 정사영의 끝점을 각 축 연장선에 그린 다음
iv) 각 기저벡터 방향의 눈금으로 좌표값을 읽는다.

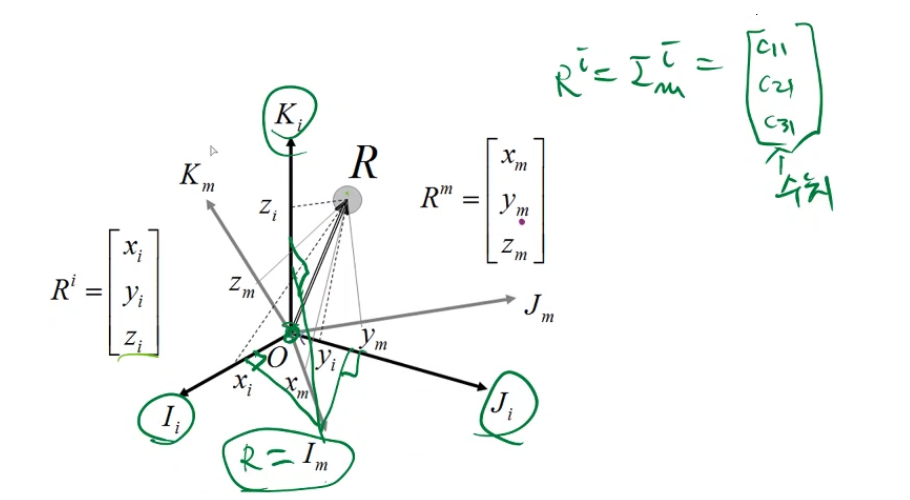
막대벡터 R과 이것을 수치적으로 표현한 좌표값 사이의 관계를 그림으로 표시한것이
그림1이된다.
관측하고자 하는 대상 R
세개의 방향은 각각 길이가 1이고 서로 직교한다.
아래첨자 a를 활용해서 Im Jm Km이 표현되어있는데
기저벡터들을 활용해서 좌표값을 읽을수가 있는데
막대벡터를 M좌표계에 대해서 좌표값을 읽는 과정을
살펴보도록 하겠습니다.
정사영을 그려보면 M좌표계에 끝점을 정사영을 그려보면
Rm=xm,ym,zm..
우리가 유사한 방법으로 Ii에 대해서 정사영을 내렸을 때
i좌표계의 두번째 기저벡터 Ji에 정사영을 내리구요
유사하게 I좌표계의 세번재 Ki좌표계에 정상영을 내리고
정사영을 내린 점까지의 길이를 구하게 되면 Ri의 좌표를 알 수 있습니다.
수치들로 고정되는 set이다==>좌표값
기저벡터, 좌표변환행렬
기저벡터는 길이가 1이며 서로 직교하는 기저벡터들이라고 지칭한다.
좌표계를 지정하는 벡터들을 해당 좌표계로 잇는 과정들을 살펴봅시다.
R이 Im일 경우

기저벡터들이 이루는 m좌표계 Im,Jm,Km
첫번째 방향에 대해서는 자기자신이 되겠죠
xm은 1이된다. 나머지는 0이된다.
R이 jm일 경우

R이 Km일 경우

다른좌표계에 표시할 경우
어떤 기저벡터들을 자기자신이 이루는 좌표들이 아니라
다른 좌표계 I좌표계 에대해서 좌표값을 잇는 경우에는 단순한 모양이 아니게 될겁니다.
R=Im일때
Jm=R일때


정사영 Jm이라고 하는 막대를 각 좌표계에대해서 읽은 c21 c22 c23라고 했는데 Jm의 길이는 피타고라스의
정리에 의해서 구할수 있다. 기저벡터의 길이는 1일것이다.
각각의 basis vector들을 좌표값으로 만들고 계산을 해봐도 길이는 1로 불변한다는것을 알 수 있다.

내적관계를 살펴보면 X의 길이와 Y의 막대의 길이가
둘 사이의 각도를 쎄타라고 하면 코사인 쎄타로 내적의 정의가 되는데 이것을 좌표값으로 만들어서
계산을 실제로 해보면 0이 됩니다.
벡터 R의 다양한



위 첨자 i는 좌표값을 읽는 기준 좌표계
Ri는 xi yi zi..
Rm xm ym zm..

위에서 유도한 식은 상당히 중요합니다.
Ri 앞에 있는것은 identity 행렬인데
Rm 앞에 있는것은 임의의 수치로 구성된 행렬








서로가 변환의 반대인 행렬은 identity 행렬을 갖는다.

좌표변환 행렬의 역행렬은 전치행렬과 동일하다.
일반적으로 역행렬은 계산량 부담이 매우 높은 연산이며 전치행렬은
각 원소의 행과 열 위치만 바꾸면 되므로 계산량 부담이 매우 낮다.
3. 단위 좌표변환 및 복합 좌표변환

'두 좌표계 사이의 좌표변환 행렬은 각 좌표계의 기저벡터들을
다른 좌표계에대해서 정사영한 좌표값을 나열해서 얻을 수 있다'
==>9가지 내적을 수행해야 되서 매우 계산이 어렵다
좌표변환행렬의 메커니즘을 이해하기 위해서는 좌표변환을 3단계로 구분하여 이해하는 것이 편리하다.
처음에는 Im과 Ii가 같았을 때
Im과 Jm을 z축을 기준으로해서 프사이만큼 회전을 할 때
두좌표계에서 동일한 관측대상 막대 벡터 R에 대해서 어떤 관계를 갖는지 따져보자
z축을 기준으로 회전시킬 때

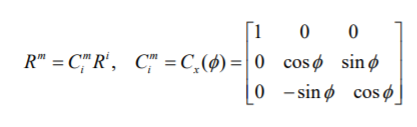

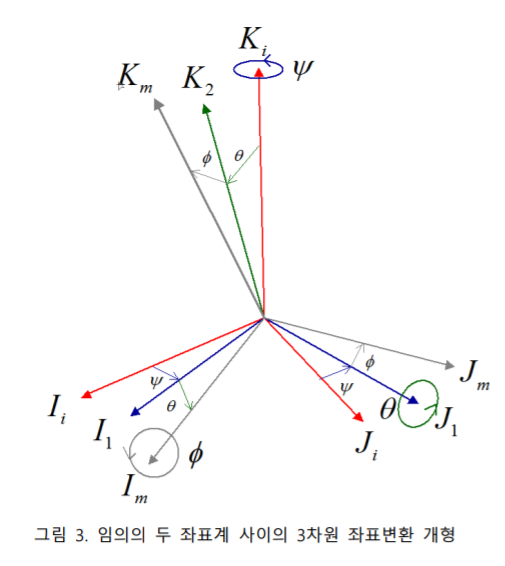
단위좌표 변환을 할 때 나타나는 기저벡터들의 방향을 살펴봅시다.
I좌표계에 기저벡터들이 있는데
최종 M좌표계의 기저벡터들을 표현하고 있는데



'2020 Fall semester > 디지털항공전자' 카테고리의 다른 글
| 디지털항공전자[4주차 QnA] (0) | 2020.09.23 |
|---|---|
| 디지털항공전자[3주차 QnA] (0) | 2020.09.16 |