확률변수(Random Variable): 표본공간 S로부터 실수 체계 R로 '맵핑' 하는 함수

베르누이 확률변수
X가 실패(0) 성공(1) 두 가지의 값만 가질 수 있으며,
P(X=1)=p
P(X=0)=1-p
X는 Bernoulli(p) 분포를 따른다고 한다.
이항 확률변수
n번의 독립적인 베르누이(p) 시행에서 성공 횟수의 분포는 Bin(n,p) 를 따른다고 한다.
이항확률변수의 확률질량변수(PMF)

이항확률변수의 특징
X ~ Bin(n,p), Y ~ Bin(m,p) 일 때,
X+Y ~ Bun(n+m,p) 를 따른다.
이항분포 Bin(n,p)
parameter n,p(n은 양의 정수, p는 [0,1] 사이의 값)에 의해서 분포가 결정됨
확률분포를 해석하는 방법
X~Bin(n,p)
의미
n번의 독립적인 Bernoulli(p) 시행에서 성공한 횟수
지시확률변수(indicator random variables)
X=X1+X2+...+Xn
X1,...Xn~iid Bern(p)
Xj=성공(1) or 실패(0)
확률질량함수(PMF)
사건의 발생확률을 구할 수 있다.

누적분포함수(CDF)
X<=x 라는 사건의 확률을 구할 수 있다.
F(X) = P(X<=x) 확률질량함수(이산확률변수에서만)

X+Y∼Bin(m+n,p)
의미
n번과 m번의 독립적인 Bern(p) 시행 중 성공 횟수
지시확률변수
X=X1+X2+...+Xn
Y=Y1+Y2+...+Ym
X+Y=ΣXj+ΣYi
PMF


초기하분포(hypergeometric distribution)로, 복원을 하지 않은 표본추출이라는 점에서 이항분포와 다르다.


문제 풀어보기

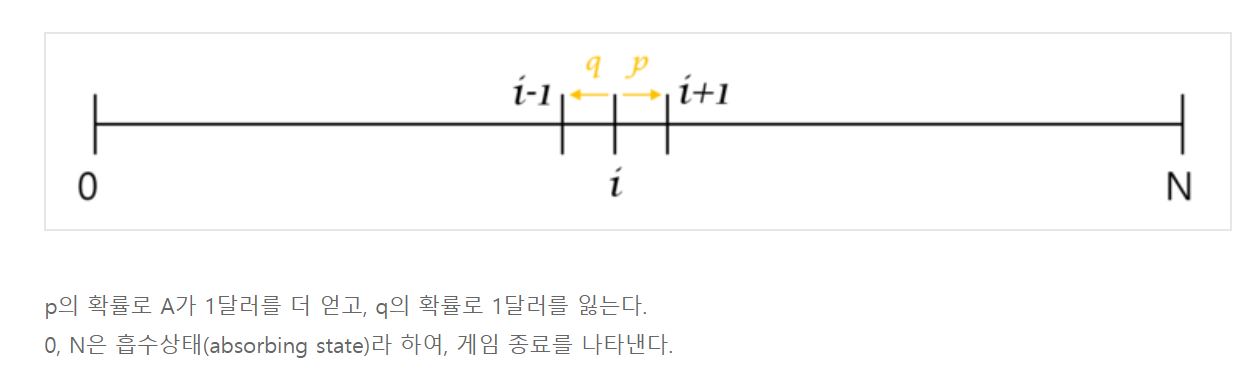
도박꾼은 각 라운드에서 1/3 확률로 1 달러를 얻고 2/3 확률로 1 달러를 잃는 게임을 반복합니다.
그의 전략은 "그가 $ 2보다 앞서면 그만두는 것"입니다.
그가 백만 달러로 시작한다고 가정 해 봅시다.
그가 $ 2 앞당길 확률이 1/4 미만임을 보여줍니다.
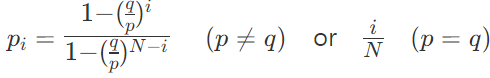

월드 시리즈에서 두 팀 (A와 B라고 부름)이 순서대로 게임을 진행하고
4 게임을 먼저이긴 팀이 시리즈에서 승리합니다.
p를 A가 개별 게임에서 이길 확률이고 게임이 독립적이라고 가정합니다.
A 팀이 시리즈에서 이길 확률은 얼마입니까?
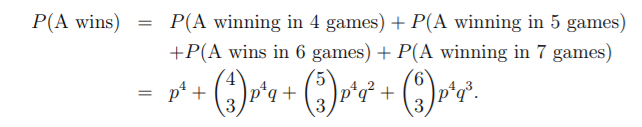
'ML > 확률론' 카테고리의 다른 글
| 수학스터디[확률통계] [기대값][기하분포][음이항분포] (0) | 2020.08.19 |
|---|---|
| 기댓값,지시확률변수와 선형성 (0) | 2020.08.12 |
| 수학스터디[확률통계]확률변수 (0) | 2020.08.07 |
| 수학스터디[확률통계] [독립][조건부확률][전확률][몬티홀][심슨의 역설] (0) | 2020.08.01 |
| 수학 스터디 [확률과 통계] [확률의 naive definition][표본추출][birthday problem] [포함배제 원리] (0) | 2020.07.24 |