Aero-Machine Learning

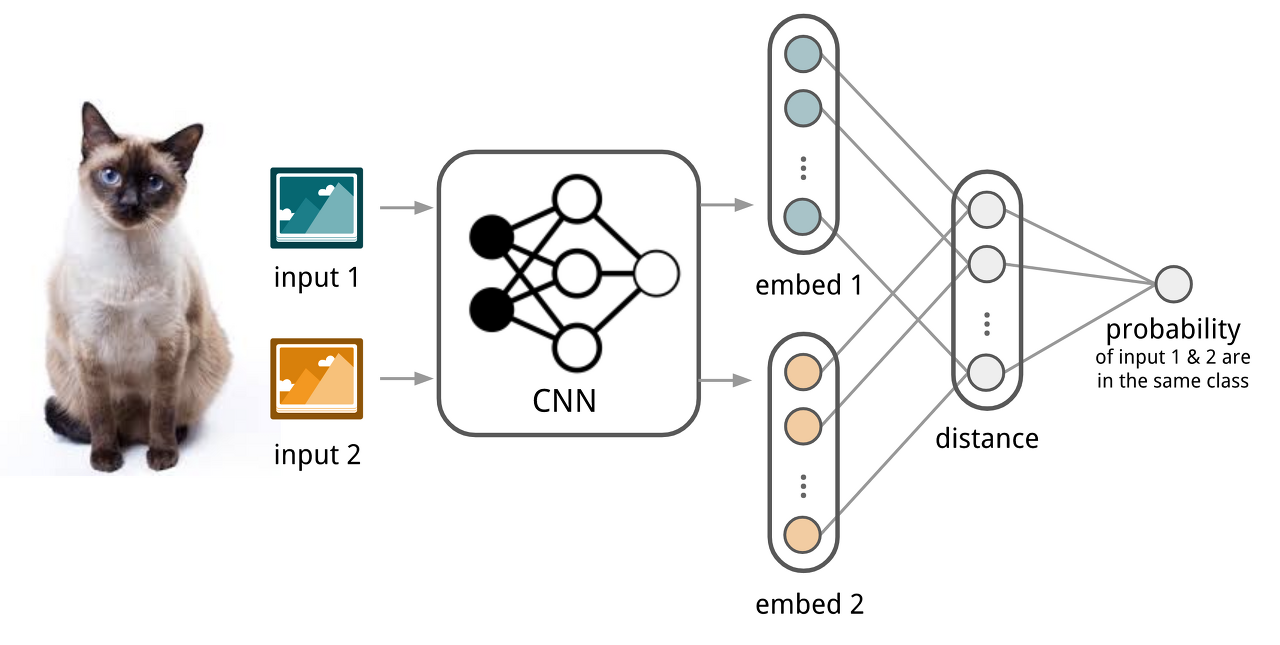
Deep face는 어떤 논문인가? What? ·주어진 이미지로부터 사람을 식별할 수 있는 CNN 구조를 묘사하는 논문이다. How? 인풋은 사람의 얼굴이다.(이미지에서 얼굴을 추출하는것이 아니다. 이미 다른 방법에 의해 얼굴은 추출되어 있는것 ) 우선 CNN 구조에 사진을 넣기 전에 2D alignment 와 3D alignment를 거쳐서 사진이 정면을 바라 보도록 해주고 (h)와 같이 새로운 측면에서의 데이터를 얻게 해준다. Face alignment / Frontalization (정렬과 정면화) 얼굴 이미지 내에서 변화를 제거하여 모든 얼굴이 카메라를 똑바로 쳐다보는 것처럼 보이도록 해준다.("frontalized") 2D alignment 얼굴에서 landmark(fiducial points...

face_recognition을 이용한 real time 얼굴 인식 2020. 3. 8. 16:31ㆍ3.5기(200104~)/출석체크 팀 2020 3월 8일 출석관리팀 DMC 탐탐 실시간으로 영상을 전송하여 얼굴 인식을 할 수 있는 face_recognition 라이브러리를 이용하여 실제 최영환과 김정민 얼굴의 영상을 인식하여 실습을 진행해 보았습니다. 최영환의 얼굴은 잘 인식되지 않았었는데 영상의 규격의 문제가 있었던것 같습니다. 갤럭시 a50 앞면 카메라를 이용하니 인식이 잘 되었고 출석체크 모델에 적용해볼 예정입니다. 참조 깃허브는 아래와 같습니다. https://github.com/ageitgey/face_recognition ageitgey/face_recognition The world's s..

torch , torch.nn, numpy (PyTorch로 신경망 처리를 위한 필수 패키지) torch.optim (효율적인 그라디언트 디센트) PIL , PIL.Image , matplotlib.pyplot (이미지를 읽고 보여주는 패키지) torchvision.transforms (PIL타입의 이미지들을 토치 텐서 형태로 변형해주는 패키지) torchvision.models (사전 훈련된 모델들의 학습 또는 읽기 패키지) copy (모델들의 깊은 복사를 위한 시스템 패키지) Matplotlib Matplotlib는 파이썬에서 데이타를 차트나 플롯(Plot)으로 그려주는 라이브러리 패키지로서 가장 많이 사용되는 데이타 시각화(Data Visualization) 패키지로 알려져 있다. 다양한 사용법이 ..

출석관리팀 발표자: 김정민 실습은 코드도 길고 첨부할 이미지도 많아서 따로 게시물을 작성하였습니다. 코드는 깃허브에서 가져왔고 중간 중간에 조금씩 수정은 하였습니다. 코랩을 이용하였기 때문에 드라이브에 마운트하여 파일을 이용하면 됩니다. 압축을 풀어서 드라이브에 업로드한다. 우선 깃허브에 있는 데이터셋으로 이용할 파일을 다운받아주고 코랩라이브러리에 저장해줍니다. 파일에는 각종 이미지가 담겨져 있습니다. 물론 주피터를 사용하신다면 본인 내장 드라이브 주소를 입력하시면 됩니다. /content/drive/My Drive/Colab Notebooks/training 위에 보이는 것이 주소입니다. 후에 언급할것입니다. #각종 라이브러리를 임포트 해줍시다. %matplotlib inline import torch..

샴 네트워크(Siamese Network) 샴 네트워크는 무엇일까? 두 개의 입력에 대해 독립적으로 두 개의 합성곱 신경망을 실행한 뒤 비교하는 아이디어이다. 샴 네트워크 구조를 간단히 설명하자면 기존의 컨볼루션 네트워크를 통해서 피처맵을 뽑아낸다. 두개의 이미지에서 피처맵을 뽑아낸 이후에 거리를 계산해 본다. 거리가 작다면 두사람이 비슷하다는것이고 거리가 크다면 두 사람이 다른 사람이라는것이다. 두 네트워크에 두 사진을 입력으로 넣고 합성곱 신경망으로 인코딩을 시킨다. 만약에 두 사람이 비슷한 사람이라면 인코딩 사이의 거리 값은 작아야한다. 만약에 두 사람이 다른 사람이라면 인코딩 사이의 거리 값은 커야한다. 위 조건을 만족시키도록 학습을 시켜야 한다. 삼중항 손실 (Triplet loss) 간단하게 ..

스터디 진행 2020년 3월 4일 DMC 탐탐 출석관리팀:김정민,박승재,최웅준,최영환,한준희 프로젝트 구체적인 주제 휴대폰 카메라를 통해서 인식한 사진을 기존에 저장되어 있던 DB와 비교하여 출석을 확인한다. 출석결과는 출석부로 보내진다. 결과는 웹(사이트)를 통해서 보내진다. 새로운 인물이 동아리에 참석하거나 인식이 올바르지 않을 때는 데이터를 보충하고 학습을 다시 시켜서 시스템을 유지 보수 가능한 모델을 구현하는 것이 목표이다. 왼쪽에 보이는 사진은 개략적인 구성도이다. 카메라, 웹서버, 데이터 서버로 나뉘어져 있다. 시스템 동작을 보여주는 다이어그램 Face database에서는 입력이 제공만 된다. 온라인으로 학습시키면서 자동으로 보수시키고 싶지만 쉽지 않을것으로 판단되어 보류하였다. 목표 기한:..

트루시니스(Truthiness), 또는 번역어로 믿고 싶은 진실, 주관적 진실이란 논증이나 논리,지적조사, 그리고 사실과 상관 없이 "직감적으로" 옳다고 느끼는 주장을 진실이라고 받아들이는 "진실"을 의미한다. 우리는 성공에 대한 잘못된 믿음들에 대해서 아무런 거리낌 없이 받아들이고 이러한 관념은 중요한 행동을 하는데 영향을 미친다. 당신은 끓는 물 속의 개구리 이야기를 들어본적 있는가 끓는 물 속의 개구리(boiling frog)는 끓는 물 안에서 천천히 죽어가는 개구리에 관한 이야기이다. 처음에 개구리가 끓는 물 안에 들어가면 깜짝 놀라 뛰쳐 나오겠지만, 만약 점점 따뜻해져 끓게 되는 뜨거운 물에 들어가게 되면 위험한 줄 모르다가 죽게 된다는 것이다. 하지만 정말 그럴까? 19세기에 이 주제와 관련한..

2019년 6월 28일 퀄컴(Qualcomm)의 인공지능 칩(AI Chip) 개발은 특허분석 결과 2010년으로 거슬러 올라간다. 그 후 2013년 10월 10일, 자사 블로그를 통해 인간의 Spiking Neural Networks(SNNs)를 모방한 뇌처럼 학습하는 프로세서(Neural Processing Unit, NPU, 신경망 처리 장치)인 '제로스(Zeroth)'를 공개했다. NPU는 사람의 뇌를 구성하는 신경망에서 아이디어를 얻었다. Qualcomm의 SNNs베이스의 NPU인 Zeroth(2013). Image source: Qualcomm 제로스는 인공 뉴럴 네트워크를 구현하기 위해 퀄컴 R&D팀이 제시한 새로운 프로세서 아키텍처로, 3가지 명확한 목적을 가지고 설계됐다. 첫째, 생물체처럼..

위의 식에서 V0 = 0인 특별한 경우를 살펴보자. 즉 전위장벽이 없는 경우이므로 자유입자에 해당하고 V0일 때 f(αa) = coska 가되어 -1~1 의 값으로 허용값이 제한된다. 이번 포스트에서 중요한것은 결정에서 전자들이 가질 수 있는 허용 에너지밴드들과 가질 수 없는 금지 에너지밴드들이 있다는 것이다. 단결정 격자를 모델링 하기 위해서 1차원 주기 전위함수를 사용한 kroning-penney 모델을 살펴보았다.

단일 전자가 완전 주기적인 격자 사이를 이동하는 것을 생각해 보자. 크로니히-페니 퍼텐셜에 대해 얻어지는 슈뢰딩거 파동방정식의 해는 식(2.1)과 같은 블록함수가 된다. I 영역과 II 영역의 퍼텐셜에너지의 차이가 있기 때문에 영역을 나눠서 파동방정식에 적용할것이다. 총에너지 E 는 파라미터 α에 포함되어있고 bV0는 β에 포함되어있다. 슈뢰딩거 파동방정식의 해는 아니지만 슈뢰딩거 파동방정식이 해를 가질 수 있는 조건을 보여주고 있다. 만약 결정이 무한정 크다고 가정하면, k는 연속적인 값을 가지게 되고, 실수이어야 한다.