확률변수와 확률질량함수는 엄연히 다른것이다.
P(X=x)+P(Y=y)
x에 관한 함수
y에 관한 함수
x+y의 확률질량함수를 구하고 싶으면
x+y가 확률변수여야 합니다.
x+y에 관한 함수가 필요한 것 입니다.
'지도는 영토가 아니다'
확률변수는 집이다.
분포는 집의 설계도 입니다.
하나의 설계도를 가지고 여러개의 집을 만들 수 있습니다.
아주 많은 다른 확률 변수들이 같은 분포를 가질 수 있습니다.
독립적일 수도 있고 독립적이 아닐 수도 있습니다.
이제 이걸 확률 집이라고 할 겁니다.
분포가 확률 집을 지을 때 쓰이는 설계도라고 하면
확률변수는 그 확률 집 중의 하나인 겁니다.
설계도는 문의 위치나 방의 구조를 말해준다기 보다는
특정 확률을 가지고 무작위로
문의 색을 빨강 혹은 파랑으로 정하는 겁니다.
확률변수는 그 집입니다.
포아송 분포
표기법
X~Pois(λ)
PMF
P(X=k)=e^-λ * λ^k / k!
k는 영이 아니다
λ는 비율 파라미터

포아송 분포의 기댓값
기댓값: 값과 확률의 곱의 합이다.

포아송 분포의 기댓값은 λ가 된다.
포아송 분포가 왜 중요할까요?
포아송분포는 실제 이산형 데이터의 모델로 가장 많고 널리 쓰이는 분포입니다.
수를 세는 응용에서 쓰입니다.
음수가 아닌 정수니까
어떤 숫자를 센다고 할 때 성공의 수를 세는 응용이라고 생각해봅시다.
이항분포처럼 성공과 실패는 일반화된 의미를 가집니다.
많은 시도를 하는데 각 결과는 성공 또는 실패입니다.
많은 시도와 아주 낮은 성공확률을 자긴 응용이어야 합니다.
한시간 안에 받은 이메일 갯수
이게 왜 포아송 분포일까
이메일을 보낼 수 있는 사람은 많다.
하지만 주기적으로 이메일을 보내는 사람이 아니면
각 사람이 당신에게 이메일을 보낼 확률은 매우 낮다.
초콜릿 칩 쿠키 안에 든 칩의 개수
쿠키 반죽으로 시작해서 칩을 몇개 만들고
모든 반죽이 초콜릿 칩인것은 아니다.
초콜릿 칩이 있을 있을 수 있는 조각은 많다.
특정 지역에서의 1년간 지진발생 횟수
Poisson Paradigm
실제로 포아송 분포를 쓰일 때는 상한이 있지만
이론에서는 무한대로 간다. k={0,1,2,3,4,5,6...}
하지만 대부분의 경우에는 추정하기 유용한 분포일것이다.
==>포아송 근사 혹은 pois Paradigm 이라고 부른다.
사건 A1,,,An
P(Aj)=pj
n은 큰수이고, pj는 작고,
각 사건들은 독립이거나 "약하게" 의존하는 경우
Aj의 발생 횟수가 포아송 분포에 근사한다고 주장할 수 있다.
여기서 람다(λ)가 포아송 분포의 기댓값이므로
Aj의 발생 횟수의 기댓값이 되는것이다.
사건이 의존적이여도 선형성에 의해 Aj의 발생횟수의 기댓값은 pj의 합과 같다.

이항분포의 포아송분포 수렴
지금까지는 각 사건이 독립적이고
각 사건의 발생 확률 p가 동일한 베르누이 분포기에
사건 발생 횟수가 p 확률의 이항분포였다.
이항분포(n,p)가 포아송 분포로 수렴한다는것을 증명해보자.
포아송 분포는 이항분포보다 훨씬 일반적이다.
즉, 이항분포를 만족하면 포아송 분포를 만족한다는것
(포아송 분포의 경우 p가 달라도 되고 조금의 의존성도 허용된다.)

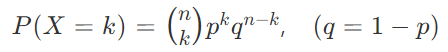
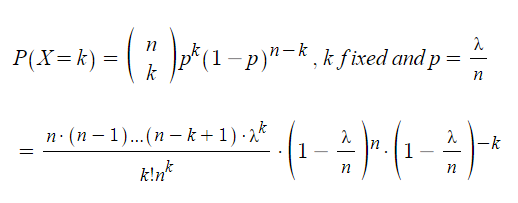
n을 극한으로 보내면
n->∞
λ/n->0
k!는 상수
n(n-1)...(n-k+1)/n^k=e^-λ



포아송분포 문제
Raindrops are falling at an average rate of 20 drops per square inch per minute. What would be a reasonable distribution to use for the number of raindrops hitting a particular region measuring 5 inches^2 in t minutes? Why? Using your chosen distribution, compute the probability that the region has no rain drops in a given 3 second time interval.
==>포아송 분포를 사용하면 좋다.
λ=average rate of 20 drops per square inch per minute*5
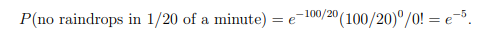
P(X=k)=e^-λ * λ^k / k!
'ML > 확률론' 카테고리의 다른 글
| 정규분포 (Normal Distribution) (0) | 2020.08.26 |
|---|---|
| 이산,연속,균등분포 (Discrete vs. Continuous, the Uniform) (0) | 2020.08.19 |
| 수학스터디[확률통계] [기대값][기하분포][음이항분포] (0) | 2020.08.19 |
| 기댓값,지시확률변수와 선형성 (0) | 2020.08.12 |
| [확률변수] [베르누이 확률변수] [이항학률변수][지시확률변수][CDF][PMF] (0) | 2020.08.12 |