
항상 임피던스를 스미스차트로 표현을 할 때는 특성 임피던스로 나눠서 정규화를 시킨다.
만능으로 만들어주기 위해서 정규화를 한다.
끝지점에서의 반사계수가 있으면 끝지점에서 반사계수가 얼마냐
부하단에서 반사 계수를 알려면
계속 원을 만들면서 원포인트 제로를 중심으로 하고
반경이 제로가 되는것을
Zin
인풋 임피던스라고 표현할것인데
부하단에서 떨어져서 측정을 하는데 부하단을 들여다 볼거야
부하단을 들여다 봤을 때 보이는
Zin은 앞에서 봤던 2.44와 똑같다.
2.43이 반사계수였고
임피던스가 반복적으로 나타나더라..
베타엘이라는것을 집어넣어 보면 베타엘이
임피던스는 2분의 람다 기준으로 반복해서 일어난다.
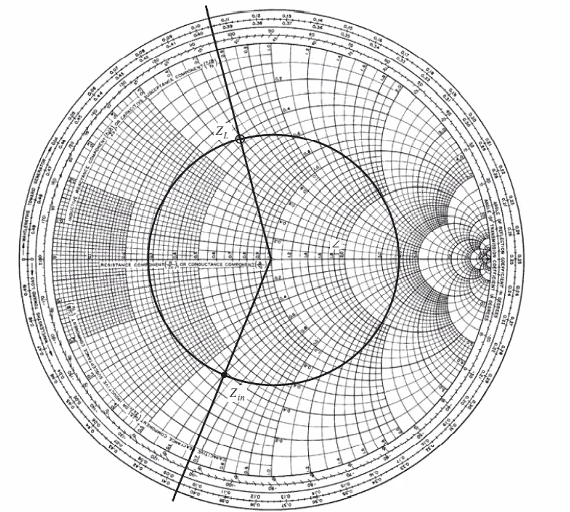
몇 람다가 걸리는가 완전히 반대쪽까지 오는데 람다/4

z스미스 차트만 선별적으로보면 그지점이 z다.
그런 장점이 있다.
Zl로부터 온 임피던스를 읽은것인데
알고보니까 Zl위치에서의 어드민턴스 값을 주더라..
y를 나타내는것이라고
람다/4 원리를 알려주고 있는것이다.
zin=1/zl=yl
2.39번 수식에 보면 감마를 무엇으로 표현했느냐
크기를 절대값으로 하고
2.44,2.91 비교합니다.
손실이 있고 없고 그 차이만 나타내는것
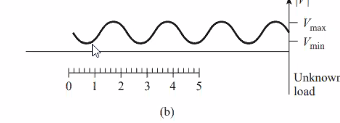
그림 2.14 a 번처럼 볼테지 그림을 그릴수 있더라
2.39번 그림을 보면
측정으로서 벌써 안것이지
세타는 l미니멈이 어디서 나오는지
l미니멈의 시작점은 어디인가?

부하단으로부터 시작해서 길이를 잰것이다.
부하단이 어디입니까?
y축 있는곳이 부하단
가상의 부하단이 여러군대 있다.
실제 연결한 다음에 부하단으로부터 얼마 떨어져 있느냐를 눈금자가 어디에
위치해 있는지 부하단을 다른곳에 위치시켜도 된다.
'2020 Fall semester > 마이크로파공학' 카테고리의 다른 글
| 마이크로파공학 [4-1] (0) | 2020.09.21 |
|---|---|
| 마이크로파공학 [3-2] (0) | 2020.09.16 |
| 마이크로파공학 [3-1] (0) | 2020.09.14 |
| THE WAVE EQUATION AND BASIC PLANE WAVE SOLUTIONS (0) | 2020.09.13 |
| FIELDS IN MEDIA AND BOUNDARY CONDITIONS (0) | 2020.09.13 |