무한 전위우물과 터널링 현상 [양자역학]

무한 전위우물 문제에 대한 파동방정식의 해

1차원 상자속 입자의 퍼텐셜, 우물 안에선 퍼텐셜이 0이고 우물 밖에선 무한대이다.

입자가 위의 그림과 같이 무한 전위우물(potential well)에 갇혀 있다고 생각해보자. 

파동방정식의해(양자화된 Ѱn)와 이 파동방정식에 대응하는 에너지 상태 En(입자의 양자 상태)을 구해보자.

 

전위우물의 경계조건(boundary condition)은 다음과 같다 

· 0<x<L  :V(x) = 0  ,Ѱ(x)

· x = 0,L :V(x) = ∞ ,Ѱ(x) = 0

 

Ѱ(0,L)≠ 0 이면 Ѱ는 연속이다. Ѱ*Ѱ≠ 0이므로 입자를 발견할 확률이 존재한다.

 

이전 시간에 다루었던 시간독립 파동방정식

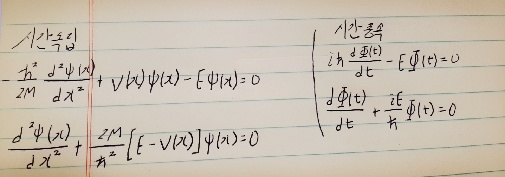
위의 시간독립 방정식에 V=0을 대입해보면 

 

Ѱ=AsinKx 로 일반해를 구할 수 있고 En=n^2x

 

미분방정식을 푼후에 경계조건을 적용하면 Ѱ=AsinKx 로 일반해를 구할 수 있고 

②번식과 ①번식을 대입해서 풀고 L이 충분히 작다고 가정했을 때 E의 값이 증가하는

형태의 양자효과(quantum effect)를 얻을 수 있다.

즉, 에너지의 크기가 특정 이산(離散)값으로만 정해질 수 있다는 것이다.

 

 

진폭 A의 결정 

Ѱ= AsinKx=Asin(nπ/L)x 임을 알고 있다.

진폭 A를 구하였고 Ѱn도 구하였다.

중간 계산과정 중에 생략된 부분

 

n에 대한 파동방정식을 정의했다. n=1,2 에 대한 파동함수와 확률밀도함수 분포를 알아보자!

n=1,n=2일때 파동함수( Ѱ)와 확률밀도 함수( lѰl²)

n=1일 때 입자를 발견할 확률은 우물 내 중앙 부근에서 최대가 되며 

n=2일 때 L의 길이가 ¼ ¾ 인 지점에서 최대임을 알 수 있다. 

n의 값이 커짐에 따라 전체 길이에서 입자를 발견할 확률이 일정해진다!

 

 

터널링 현상

고전역학에서의 에너지 장벽

고전역학에서는 장애물을 향해 공을 던지면 그 공은 장애물을 치고 다시 돌아온다.

공의 에너지가 장애물을 뚫고 지나갈 만큼 크지 않기 때문이다.

물리학자들은 이런 현상을 에너지 장벽(potential) 이라고 부른다. 

 

하지만 미시적 원자 세계에서는(양자역학에서) 입자의 에너지가 에너지 장벽의 에너지보다

작더라도 장벽을 통과할 수 있는 확률이 있을 수 있다.

 

이러한 현상을 터널링(tunnelling) 현상이라고 한다.

 

실제 고체 내부의 전자를 고려해보자 장벽의 높이는 유한하며 장벽의 두께 역시 유한하다 

즉, V(0,L) = V로 규정할 수 있고 유한한 폭 W로 정의한다. 또한 이때 Ѱ 이다.

슈뢰딩거의 가정에서 처럼 Ѱ'(Ѱ의 기울기)는 연속이어야 하므로 

장벽 안과 밖에서 슈뢰딩거, 즉 입자를 발견할 확률이 존재한다.

 

 

 

<요약>

1.슈뢰딩거의 파동방정식은 고전역학의 에너지 관계로부터 얻을 수 있으며,

경계조건을 대입하여 자유전자, 무한 전위우물 및 원자 내에서의 파동방정식을 구할 수 있다.

2. 에너지 장벽을 뛰어넘지 않고 통과하는것을 터널링 현상이라고 한다.