
거시적인 전자기 현상은 Maxwell에 의해서 발표된
맥스웰 방정식으로 기술된다. 이 연구는 그 당시의 전자기학 이론들을 요약한것이며
전기적인 변위 전류(displacement current)의 존재에 대한 고찰로부터 이론적으로 가설을 세웠으며,
그 후에 Hertz와 Marconi에 의해서 전자파의 전파 현상을 발견하였다.
Maxwell의 연구는 Gauss,Ampere,Faraday 등에 의해서 밝혀진 경험적이고 이론적인 주요부문에 근거를
두고 있다. 전자기학의 첫 번째 과정은 보통 이러한 역사적인 접근방식을 따르는것이다.
맥스웰 방정식이 제시되고
경계조건과 유전체와 자성체의 효과에 대해서 다룰것이다.
마이크로파 공학에 있어서 파동 현상(wave phenomenon)은 기본 명제이며,
이 장의 많은 부분은 평면파(plane wave)에 대해서 다루고자 한다.
평면파는 여러 형태의 전자파 중에 제일 간단한 형태이며 전자파의 전파(wave propagation)와 관련한 많은 기본적인 특성들을 묘사하는 데 수식을 쉽게 표현할 수 있다.
독자가 전에 평면파에 대해서 공부하였다고 할지라도
이 책에서는 기본원리를 많이 강조할 것이며 아마 독자가 전에 본적 없는 개념들에 대해서도 소개하려고 한다.
Maxell's Equation in differential form

E:전기장의 세기 [V/m]
H:자기장의 세기 [A/m]
D:전속밀도 [Coul/m^2]
B:자속밀도[Wb/m^2]
M:(가상의)자기전류밀도[V/m^2]
J:전기전류밀도[A/m^2]
ρ:전하밀도[Coul/m^3]
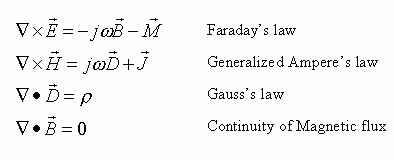
1. 변화하는 전기력(electric)이 발생하면 항상 그에 수직하는 자기력(magnetic)이 발생하고
2. 그 역도 성립한다
3. 체적 내부에 전하가 있을때 체적의 표면을 관통하는 전기력선의 합은 체적내부의 전하량하고 같다.
4. 닫힌 체적의 표면을 관통하는 자기력선의 합은 항상 0이다.
맥스웰 방정식을 통해 알 수 있는 전자기력의 원리는 결국 다음과 같다.
1. 변화하는 전기력과 자기력은 항상 쌍으로 존재하면서 수직으로 전자기력을 구성한다.
2. 전하가 존재하면 그 양에 비례하는 전기력선이 발생한다.
3. 자기력은 항상 Closed-Loop를 이루게 된다.
전자계의 원천(sources)들은 전류 M,J와 그리고 전하 ρ이다.
자기전류 M은 단지 수학적인 편리함을 위한 가상의 자계 전류원이다.
자기전류의 실제 근원은 항상 전류의 루프 또는 실제 자하(자기적인 단독 자하의 존재는 알려져 있지 않다.)의
흐름에 반대 방향인 자기 쌍극자와 유사한 형태이다.
자기전류는 완전성을 위하여 개구면을 취급하는 제4장에서 가끔 사용할 것이다.
전류는 실제로 전하의 흐름이므로 전하밀도 ρ가 전자계의 궁극적인 근원이다.
자유공간에서 전계,자계와 선속밀도 사이에는 다음과 같은 간단한 관계가 성립한다.

µ0 = 4π × 10−7 henry/m is the permeability of free-space, and
ε0 = 8.854 × 10−12 farad/m is the permittivity of free-space.
u0=자유공간 투자율을 의미한다.
ε0=자유공간의 유전율이다.
다음절에서 자유공간이 아닌 매질은 이들의 구조적인 관계에 어떤 영향을 미치는가에 대해서 알아볼 것이다.
맥스웰 방정식은 선형적이지만 서로 독립적은 아니다.
예를 들어

임의의 벡터의 회전에 대한 발산은 0이므로

자유로운 자하는 존재하지 않음으로 ∇ · M¯ = 0
따라서 ∇ · B¯ = 0, 혹은

이 된다.



이 방정식은 전하가 보전성을 갖고 있다는 것 혹은 전류가 연속적임을 나타내고 있다.
∇ · J는 한 점에서 전류의 외향적 흐름을 표현하며
∂ρ/∂t는 동일한 점에서 시간에 따른 전하의 증대를 표현하고 있기 때문이다.
This equation states that charge is conserved, or that current is continuous, since ∇ · J¯ represents the outflow of current at a point, and ∂ρ/∂t represents the charge buildup with time at the same point.
It is this result that led Maxwell to the conclusion that the displacement current density ∂D¯ /∂t was necessary in (1.1b), which can be seen by taking the divergence of this equation
맥스웰이 식 이 ∂D¯ /∂t가 필요한 이유이다.

위 식에 발산을 취함으로써 설명되어질 수 있다.
Maxwell’s equations in Integral form



1.4에 Q는 폐곡면 S로 둘러싸인 체적 V 내에 포함된 총 전하를 나타낸다.



여기서 M항을 제외하면 Faraday 법칙의 일반형이 되며
이는 키르히호프 법칙의 기본 원리가 된다.

C는 그림에서 표면 S 주변의 폐경로를 나타낸다.
Ampere 법칙은 Stoke의 정리를 적용하면 다음과 같이 표현할 수 있다.

I = S J¯ · ds¯ 는 폐곡면 S를 통과하는 총 전류의 흐름이다.

Maxwell’s equations in phasor form
위 방정식들은 임의의 시간에 대해서 유효하지만
대부분 우리의 연구는 정상상태(steady-state) 조건을 가정한 시간에 따라서
정현적(sinusoidal) 또는 고조파(harmonic)적으로 변하는 계에 한정될것이다.
The above equations are valid for arbitrary time dependence, but most of our work will be involved with fields having a sinusoidal, or harmonic, time dependence, with steadystate conditions assumed.
이러한 경우에 있어서 페이저(phasor)의 표기법이 매우 편리하므로
모든 field의 양은 시간 의존성을 의미하는 e^jωt를 갖는 복소벡터로 가정하며
필기체 대신 로마체 활자로 표기할 것 이다.
그러므로 xˆ방향의 전형적인 field는

A는 직폭이고 ω는 각주파수,φ 는 t=0에서의 wave의 위상 기준(phase reference)이며
다음과 같은 페이저 형태를 갖는다.
where A is the (real) amplitude, ω is the radian frequency, and φ is the phase reference of the wave at t = 0

이 책에서는 cosine 기준의 페이저를 가정하며, 페이저 양에서
실제 시간에 따라서 변화하는 양으로의 변환은 페이저에 e^jωt를 곱하고
실수항을 취함으로써 얻어진다.

위식에 그 위의식을 대입하면 그 위의 식을 얻을 수 있다.
페이저 표기법을 사용하는 경우, 모든 항의 공통항인 e^jωt은 보통 생략한다.
전력과 에너지를 취급할 경우, 가끔 시간적 평균값에 관심을 갖게 되는데
이는 시고조파계(time harmonic field)에서 매우 쉽게 찾아 볼 수 있다.


시간 의존성을 e^jωt를 가정하면 시간에 대한 미분은 jω로 애치할 수 있으므로 Maxwell 방정식의 페이저 폼은

임의의 주파수 ω에 대한 Maxwell 방정식의 해를 임의의 시간에 대한 해로 변환시키려면
푸리에 변환을 사용하면 된다.
J와 M은 각각 A/m^2, V/m^2의 단위를 갖는 체적 전류 밀도들이다.
그러나 대부분의 경우 실제 전류는 평판 전류(sheet current),
선전류(line current) 무한소 다이폴 전류 (infinitesimal dipole current)의 형태로 존재한다.
이와 같은 특별한 형태의 전류 분포들은 델타 함수를 사용함으로써 체적 전하 밀도로 나타낼 수 있다.
그림 1.4s는 이러한 과정을 전기 자기적 전류에 대해 적용한 예를 나타내고 있다.

Diffrential form, Integral form, Phasor form

'2020 Fall semester > 마이크로파공학' 카테고리의 다른 글
| THE WAVE EQUATION AND BASIC PLANE WAVE SOLUTIONS (0) | 2020.09.13 |
|---|---|
| FIELDS IN MEDIA AND BOUNDARY CONDITIONS (0) | 2020.09.13 |
| 마이크로파공학 [2-2] 수업 정리 -수정중- (0) | 2020.09.09 |
| [마이크로파공학] [2-1] (0) | 2020.09.07 |
| [마이크로파공학] [1-2] (0) | 2020.09.07 |