


curl H는 j를 시그마를 포함해서 표현한다.
로스리스 미디움에 입실론 대신 입실론 c를 사용해서 표현하면 된다.
입실론 c를 구체적으로 표현하면
complex 입실론에 의해서 k값도 컴플렉스로 나타난다.
k가 컴플렉스 넘버이다.

리얼 파트와 이메지너리 파트를 나누려고 한다면
k를 그대로 로스가 있는 미디움에서
k를 그대로 쓰는 대신에 감마라는 컨스턴트를 도입한다.
감마는 컴플렉스 넘버가 되는데
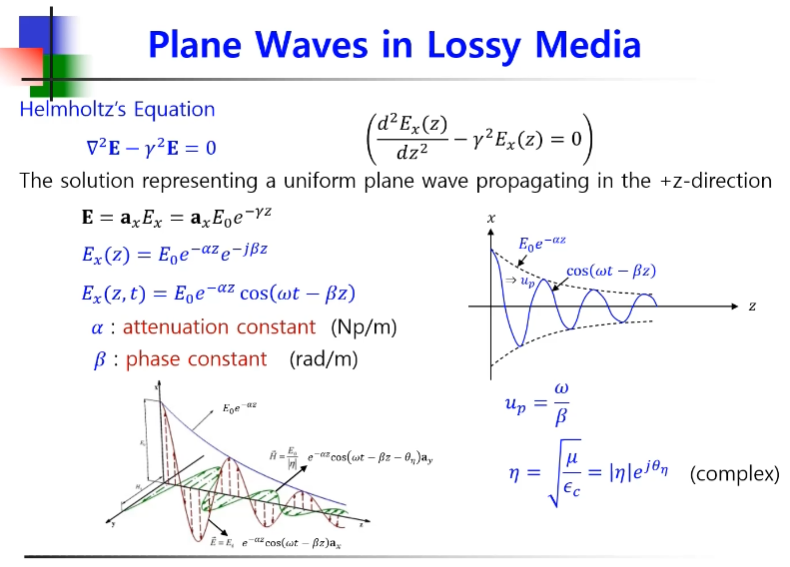
감마는 식으로 표현한 헬름홀츠 식은 위와 같이 바뀌게 됩니다.
e^-az는 크기가 아니다.
E0에 포함해줄 수 있다.
뒤에 있는 -jBz가 파동을 표현한다.
jk와 비슷한 역할을 하는것이 베타B 이다.

베타가 웨이브 넘버 역할을 한다.
알파는 감쇠상수 역할을 한다.
파동의 역할을 하는것은 베타에서 파동의 역할을 하는것은
속도=w/B
파장도 베타로부터 나타나게 된다.
베타를 구해줘야 감마로부터 A와 B를 구해서
에타를 보면 E와 H의 크기의 비가 되는데
에타가 입실론 c가 컴플렉스 넘버여서 에타도 컴플렉스 넘버로 나타난다.
에타의 위상이 추가가 되야 한다.
자기장과 전기장이 임피던스가 리얼이면 위상이 같다.
하지만 컴플렉스가 되면 전기장과 자기장의 위상이 달라진다.
로스리스에서는 위상이 같았죠
하지만 컴플렉스에서는 위상이 차이가 난다.

로시한 미디움은 시그마 variation이 굉장히 커서
low loss 일 때
좋은 절연체이긴 하지만 완전하지는 않은
그러한 절연체를 얘기할 때

허수부분이 작기 때문에
이항정리를 이용해서 정리를 하면

베타를 보면 베타는 허수부분이니까 첫번째 항과 세번째 항을 더한것이 베타가 된다.
베타는 오메가에 비례해서
dispersionless 디스퍼션이 없는 미디움이다.
주파수에 상관없이 일정한 속도를 가지는 수신기에서도 송신기에서도
같은 스펙트럼을 수신할 수 있다.
디스퍼션이 있는 미디움에서 주파수에 따라서 속도가 달라지면
신호의 왜곡이 발생이 된다.

오메가와 k가 서로 비례하면
디스퍼션이 없다고 얘기할 수 있다.
low로스 일 때 항은 추가는 되지만 오메가에 비례해서
w가 constant가 된다. 그래서 디스퍼션이 없다' 라고 한다.

컴플렉스로 나타나게 되는데
에타가 컴플렉스가 되면 E와 H에 위상 차이가 난다.
입실론 더블 프라임은 매우 작은 값이어서 약간의 위상 차이가 난다.

속도를 보면 주파수에 관계가 없다=>디스퍼션이 없다(로우 로스일 경우)

굿 컨덕터는 완전한 도체 (시그마가 무한대)는 아니지만 시그마가 클 경우
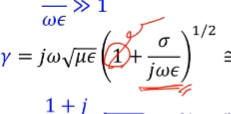
1은 무시할 만큼 큰 값이 된다.
리얼 파트가 +인 경우만 알파가 +인 경우만 고려를 하면
베타가 속도와 연관이 되는데
베타가 f에 비례하지 않고 스퀘어 루트 f에 비례하기 때문에
디스퍼션이 있다.
주파수에 따라서 디스퍼션이 발생한다.
시그마에 스퀘어 루트에 비례해서 알파도 큰값으로 나타난다.
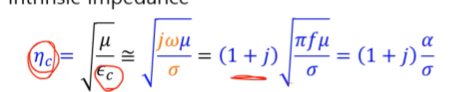
에타c가 위상이 45도 정도 되는데
자기장과 전기장의 위상차가 45도가 난다.
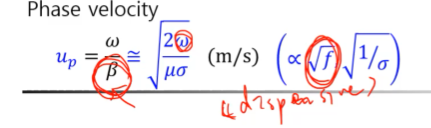
위상 속도를 보면 속도는 베타에의해서 결정이 되는데
속도가 주파수에 따라서 달라지기 때문에
디스퍼스가 있다.

컨덕터에 전기장이 가해지면 매우 빠른속도로 줄어들게 된다.
표면에만 필드가 약간 있고 표면에만 전류가 흐르게 된다.
표피두께를 설정하게 되는데 크기가 e-1의 두께로 줄어들게 되는데
z값을 표피 두께라고 한다. 1/알파
표피두께는

로시 미디움은 주파수의 영향을 받는데
표피두께 안으로 들어가면 전기장이 거의 없다.==>더 깊숙히 가면 신호도 못받음

시그마가 매우 높을 때
속도가 720m라는 것은 음속에 가까운데
페이저 속도가 매우 느려진다.

표면에만 전류가 흐른다.

잠수함과 통신할 때 주파수를 낮게하면 침투할 수 있다.
하지만 높은 주파수를 사용하면 잠수함과 통신 x

100cos(10^7 pi t)
주파수는 w/2pi = 5 x 10^6 Hz
감쇠상수는 얼마인가 =>8.89 =베타

E와 H의 타임 도메인을 구하라


H를 구할 때는 타임도메인에서 바로 나누면 안되고
페이저 도메인에서 임피던스로 나눠주고
페이저에서 임피던스를 나눠줘서 타임도멘인으로 나눠준다.
전기장과 자기장이 다르다!

전리층문제 혹은 플라즈마문제에 대해서 알아보도록 하겠습니다.
고도 50~500km되는 위치에서 전리층이 존재하는데
전리층에는 free 전자와 positive 이온으로 이루어져 있다.
분자나 원자에 자외선이 가해지게 되면
전자들이 자유전자로 바뀌어서 전자와 이온이 섞여 있는 상태가 된다.
전리층도 그렇고 전자와 이온의 밀도가 같을 경우 이것을 플라즈마라고 한다.
이온같은 경우 속도가 느리고 전자는 속도가 빠른데
전자의 움직임을 가지고 플라즈마를 분석 가능하다.
전기장을 가했을 때 어떤 일이 발생할까

전자가 이동할 때 -eE=.d^2x/dt^2
-mw^2x
x=e/mw^2 E

전자가 움직이게 되는데
이온이 가만히 있으면
분극이 발생한다.
만약에 지금 전기장 밀도가 있으면 폴로라이제이션 벡터를 구할 수 있다.
P=Np이렇게 구할 수 있다.
E와 D 사이 관계가 위와 같으니 좀 전에 구한 P를 대입을 하면

오메가 p를 플라즈마 앵귤러 프리퀀시라고 부르는데
2파이로 나눠주면 그냥 frequency가 됩니다.


등가 유전율을 생각하면
오메가와 오메가 피가 같으면 입실론 p가 영이 되는데
그럼 E는 존재하는데 D가 0가 되는 현상이 발생한다.
감마는 f가 fp보다 작으면 두번째 항이 1보다 커지게 되서
허수가 된다. 그렇다면 감마가 리얼이 된다. (앞에있는 j와 합쳐져서)
프로파게이션이 일어나지 않고 감쇠만(베타는 0) 된다.
플라즈마에 신호를 가하면 전파는 안되고 줄어들기만 한다.
차단주파수다' 특정 주파수 이상이 되지 않으면 전파가 일어나지 않는다.
에타를 보면 에타가 주파수가 fp보다 작아지면
에타가 이메지너리 j 섬띵으로 된다고 하면
임피던스가 허수가 되면 인덕터나 커패시턴스
z=jx 에너지를 소모하지 않는다.
에너지가 흘러들어가지 않는다.
플라즈마가 있는데 전기장과 자기장의 위상 차이가 90도 차이가 나면
전력전송이 이루어지지 않는다는 얘기다.
플라즈마 속으로 전력이 흘러들어가지 못한다는 이야기이다.
에타는 이메지너리가 되고 감마는 리얼이되서 전송이 이루어지지 않는다.
그래서 플라즈마 주파수보다 낮아지면 전송이 일어나지 않는다는 말이다.
더 높아지면 전송이 일어나게 되겠죠.

np가 허수가 되서 파워의 전송이 일어나지 않는다.
fp를 cutoff frequency가 일어난다.
D가 없는 상태에서 E가 있다. 플라즈마 오실레이션이라고 한다.
D가 없는 상태에서 E가 자체적으로 발생하는것
fp를 정리하면 fp=9root N
fp가 0.9에서 9MHz 범위가 된다. 이것이 차단 주파수가 된다.
레이어가 낮으면 차단주파수가 낮고 레이어가 높으면 차단 주파수가 높아지게 된다.

지상에서 전리층을 활용한다면 통과를 못하죠 그럼 반사가되죠
지상파로는 도달하기 어려운 그런 경우에도 전리층 반사를 이용해서
로우 프리퀀시를 이용하게 되면 지구의 아주 먼곳에 있는곳 까지 통신이 가능하다.
예제 8-5를 보면 위성이 집으로 귀환할 떄 전리층을 통과해서
플라즈마를 발생하게 되죠 전기장 밀도가 2x10^8일때
위상이 귀환할 때는 fp가 127 MHZ까지 올라간다.

이번시간에는
도플러 이펙트
TEM WAVE
평면파 편파
로시 미디움의 플레인 웨이브 전송
+플라즈마 포함해서
얘기를 했습니다.
'RF 시스템 설계 > 전자기학II' 카테고리의 다른 글
| 전자기학 II 기출 (0) | 2020.10.20 |
|---|---|
| 전자기학 II [정리] [Static magnetic field~PLANE WAVE] [6.1~8.3] (0) | 2020.10.18 |
| Plane Electromagnetic Waves-[1] (0) | 2020.10.07 |
| Plane Waves (0) | 2020.10.04 |
| Time-Harmonic Fields (0) | 2020.10.04 |