

지난 시간에 페이저에서는 위상 지연으로 나온다.

임의의 방향으로 진행할 경우 어떻게 될 것인가?
이런 것에 대한 식을 유도하겠습니다.



도플러 이펙터는 송신기와 수신기가 있을 경우 송신 주파수와 수신주파수가 일치하겠죠
송신기나 수신기가 움직인다고 했을 때
수신주파수가 송신 주파수와 다르게 나타난다.
멀어지면 더 낮게 가까워지면 더 높게 나타나는 현상에 대해서 유도할게요.
T는 송신기가 되고 R은 수신기가 됩니다.
세타 방향으로 이동을 할 때
t=0일 때 도착하는 시간은 언제인가?
t1=r0/c
송신기가 이동할 때 델타 t라는 시간이 지나면 T'
T'에서 송신되었을 때 수신되는 시간 t2
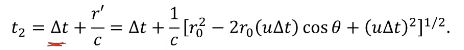
r'은 삼각형에서 코사인 법칙을 이용하면 되겠죠
거리가 멀리서 이동하기 때문에 r0가 이동하는 거리에 비해서 크다고 생각하면
r0를 바깥으로 뺄수가 있는데 그렇게 되면 세 번째 항을 무시하고
1/2승은 이항전개를 하게 되면 그냥 치수를 첫 번째 항만 생각해서 넣게 되면
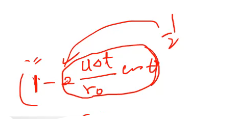


신호의 간격이 수신신호와 송신 신호 사이의 시간 차이를 생각해보면
t2-t1
송신기에서 델타t'

델타 t를 송신기의 주기다.
수신기에서 수신된 신호의 주기가 되는데

수신 주파수가 f(u/c) 만큼 주파수가 올라간다.
이것을 도플러 frequency만큼 올라간다.
도플러 주파수는 속도에 따라서 수신 주파수에 도플러 주파수가 다르게 나타난다.
속도를 가지고 도플러 레이더의 중요한 원리가 된다.

횡방향 전자기파
진행방향에 대해서 단면 방향 즉 횡 방향으로 전기장과 자기장의 벡터가 향하는 전자기파

전기장과 자기장이 대표적인 TEM이 된다.
진행방향에 대해서 Transverse electromagnetic waves
TE wave도 있고 TM wave도 있다.
uniform plane wave 자유 공간을 진행하는 임의의 방향
진행방향이 z 축이라고 해도 x방향이나 y방향일 수도 있고 어쨌든 횡이면 된다.
진행방향이 z방향이어야 한다는 것도 없고
z방향으로 진행하는 plane wave
임의의 방향으로 진행하는 유니폼 플레인 웨이브는 어떻게 표현하는가?
kx ky kz는 어떤 값을 갖게 되며 어떤 관계가 있겠는가?
우선 설루션이 헬롬 홀츠식을 만족해야 합니다.


k벡타를 정의하면


위상이 constant가 되는 평면을 생각해보면
k.R이 어떤 의미를 가졌는가
k벡터가 있을 때 R이 임의의 위치 벡터가 될 텐데
k.R이 일정한 것이 constant 평면이 된다.
k.R 혹은 an.R 이 constant 한 평면이
위상이 균일한 평면이 된다는 것을 알 수 있다.
직각인 방향으로 웨이브가 진행하니까 k방향으로 웨이브가 진행한다는 것을 알 수 있다.
an이 전파방향을 나타낸다는 것이죠.
k벡터는 wavenumber와 진행 방향을 나타내는 것입니다.

k벡터라는 것은 각각의 성분을 나타내는 것입니다.
우리가 타임 도메인에서 마찬가지로 k.R로 풀어쓰게 되면 위상과 시간과 포지션이 변화한다는 것을 알 수 있다.
플레인 웨이브가 세타의 방향으로 진행한다고 했을 때
k벡터를 먼저 구해주면 평면파의 표현식을 쓸 수 있다.
k벡터를 구해주게 되면 k값을 가지고 an방향이 되는데
ax방향으로 kx
ay방향으로 ky


k벡터의 직각인 방향으로 equivalent space가 나타나게 되고
k는 웨이브의 진행방향 + k의 크기를 나타내는 것
k벡터를 표현해서 그 방향으로 진행하는 평면파를 표현할 수 있다.

E0는 진폭==> 다이버전스는 0
두 번째 항만 살아남는다.

델 오퍼레이터 대신 -jK를 하면 된다!

결과적으로 k와 E0를 닷 프로덕트 하면 0이다.
=> k벡터와 E0는 직교한다는 것을 알 수 있다.

앞에서 결과를 보는 것과 같이


자기장은 어떤 관계가 있는가?
자기장의 크기는 1/에타 가 됩니다. 일종의 임피던스가 되는 것이죠.
방향은 an크로스 E의 방향이 되는 것입니다.

이러한 결과로부터 an방향으로 진행하는 플레인 웨이브에 대해서
E ㅗ H
E X H ll an

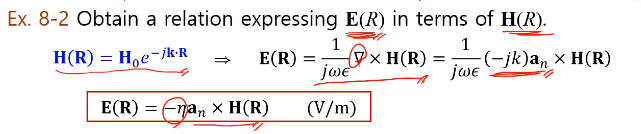
임의의 방향으로 진행하는 TEM
진행방향에 대해서 k벡터
an 방향으로 k값을 가지는 k벡터를 구하고
그쪽 방향으로 진행하는 평면파의 위상 관계를 구할 수 있고
E ㅗ H이며, 서로 유도할 수 있다.

평면파의 편파에 대해서 알아보도록 하겠습니다.
편파는 전기장의 벡터의 행동을 나타낸다.
전기장 벡터의 행동을 나타낸다.
수직 편파와 수평 편파로 나뉜다.

선형 편파
지금까지 해왔던 것들이 선형 편파가 됩니다.
z=0 평면에서 시간에 대해서 어떻게 변하는지를 보면 선형 편파인지 확인할 수 있다.

방향은 일정하면서 크기가 커졌다 작아졌다 하는 것을 선형편파라고 합니다.
굳이 x방향으로만 있으라는 법은 없고 y방향으로 있을 수도 있고
비스듬히 있을 수도 있습니다.

같은 위상으로 진행될 경우 선형 편파다.
각도 알파의 방향으로만 커졌다가 작아졌다 하는것을 알 수 있겠죠
편파는 선형으로만 한쪽 방향으로만 움직인다.


원형편파는 방향이 크기는 일정하며 방향만 회전하는 그런 벡터이다.
두 개의 직교하는 편파가 동시에 존재하며 두개가 합쳐지는데 위상이 90도 차이 날 경우
하나는 x방향 하나는 y 방향인데 90도로 위상이 늦거나 빠르거나 할 때
타임 도메인에 대해서 두개의 벡터의 합으로 표현할 수 있습니다.
알파의 크기를 구하게 되면 wt가 된다.
z 축을 바라봤을 때 우측으로 회전하게 됩니다.(들어가는 방향으로 생각했을 때)

LHCP는 y가 위상이 90도 빠를 때 나타난다!


공간 측을 따라서는 LHCP
시간축을 따라서는 RHCP가 된다. (z0=0)?




크기가 서로 다르고 위상이 90도 차이 날 때 타원 편파가 나타난다.
대부분 원 편파를 원하는데 x축과 y축을 똑같이 만드는게 어려워서
달라지게되면 타원편파가 된다.

위상 차이가 90도가 아닐때 좌표축이 일치하지 않는 타원 편파가 나타난다.
AM:수직 편파

TV:수평 선형 편파

FM:CP

들어오는 방향에 대해서 가급적 직각인 방향으로
GPS:RHCP


RHCP LHCP를 통해서 임의의 편파를 나타낼 수 있다.
우측 원형편파의 페이저 표현식과
타임도메인의 표현식을 쓰고
z=0평면에서 t에 따라서 변화하는 형태를 그림으로 그려서 제출하시길 바랍니다.
'RF 시스템 설계 > 전자기학II' 카테고리의 다른 글
| 전자기학 II [정리] [Static magnetic field~PLANE WAVE] [6.1~8.3] (0) | 2020.10.18 |
|---|---|
| Plane Electromagnetic Waves-[2] (0) | 2020.10.07 |
| Plane Waves (0) | 2020.10.04 |
| Time-Harmonic Fields (0) | 2020.10.04 |
| Maxwell's Equations & Wave Equations (0) | 2020.09.26 |