

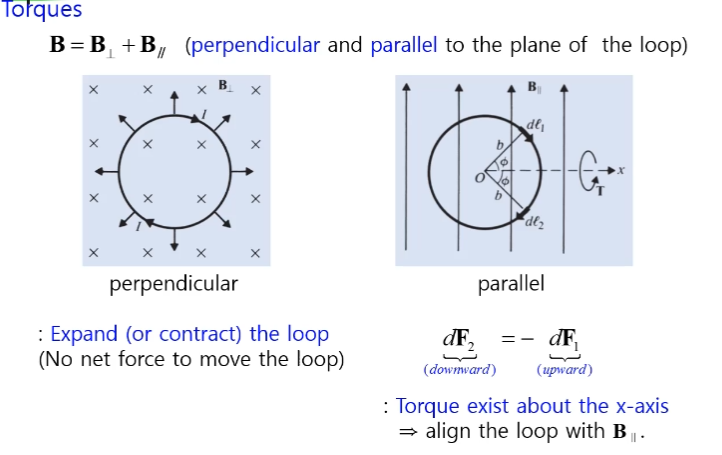
자기장내 루프에 전류가 흐르고 있을 경우 힘을 어떻게 받는가?
폐루프를 수직으로 통과하는 성분+수평으로 통과하는 성분
두가지 성분이 토크에 미치는 영향은 다르기 때문에
perpendicular

perpendicular루프의 평면에 대해서 직각인 방향으로 지나가는 성분은
퍼펜딕큘러 성분이다.
미소길이 IDL에 대해서 작용하는 힘을 보면 dFm=IdlxB
바깥으로 나오는힘이 되겠죠 모든 위치에서 모두 바깥으로 나오게 된다.
전류와 자기장이 일정하면 모두 바깥으로 나가기 때문에
전류의 방향이 반대로 향하면 안으로 들어오는 힘이 작용하게 됩니다.
NET FORCE가 0가 되서 움직이지 않고 회전도 발생하지않는다.
수직으로 지나가는 자기장은 루프의 움직임에 영향을 주지는 않는다.
Parallel

아래쪽에 있는 아래쪽 써클의 반은 들어가는 방향으로 힘이 작용하고
위쪽은 나오는 방향으로 힘이 작용하게 됩니다
x축을 중심으로해서 회전력(토크)가 발생한다.
dF2와 dF1은 반대방향으로 작용==>토크가 발생합니다.
회전을 해서 수평으로 자기장을 맞게되면 토크가 0가 됨
==>토크가 0가 될 때 까지 작용한다
Differntial torque produced

토크의 방향은 x방향으로 향하고
ax방향으로 토크가 작용하게 되고
힘과 X축과의 거리가 BSINΦ
dl이라고 하는것은 바꿀 수가 있다.

토크를 이렇게 쓸 수 있다.
Total torque
sin^2 적분
적분값이 pi/2
I(파이 b^2)=m
m벡터 다이폴 모멘트가 됩니다.
식을 보니까 m의 크기랑 같더라
B의 방향은 a와의 방향이고
an은 -az방향이 된다.
-az와 x ay =ax
결국 an벡터가 -az가 된다.
ay B paraller
토크를 보니까 토크는 결국 m에다가
B paraller 쓸 수 있다.
그러면 B pallere
mx(B +Bㅗ)
ㅗ는 있으나 마나 해서

자기장이 유니폼할 때만 위의 식을 쓸 수 있다.


Ex. 6-22

퍼펜틱은force와 토크에도 영향을 끼치지 않습니다.
z방향 성분 Bㅗ는 제로가 됩니다.
F1이 들어오는 방향
네개를 합치면 퍼펜틱 큘러에 의한 성분이 0가 된다
토크도 제로가 된다.
Parallel component
axBx+ayBy가 평행 성분이 됩니다.
ax방향 성분에 크로스하면 페러렐 성분이 됩니다.
원에 대해서 대응하는 위치가 3번인데
전류방향이 반대가 되서 F3=-F1입니다
F2는 -ay방향으로 전류가 흐르고 be parallel
F2=-F4
F1은 az방향으로 나오는 방향
F3는 들어가는 방향
==>x방향으로 회전력이 발생
F2는 az로 나오는 방향
F4는 들어가는 방향
==>-ay방향으로 토크가 발생하게 된다.

두개의 방법으로 구할 수 있다.Net Force:F1+F2+F3+F4=0
넷 force는 0이 되지만 회전력은 남게 된다.
전체 토크는 두개를 합친것이 된다.
Direct-current (d-c) motor

폐루프에 전류를 흘려서 회전력이 작용을 하게 되는데
토크를 이용해서 x축방향으로 회전력을 만들어낸다.
여러개 폐루프를 감아서해보면 폐루프를 지지하는것을
아마추어=>회전자
줄이 한바퀴만 감겨져 있으면 어떤 회전력이 생길까?
단면을 보면 S극과 N극을 볼 수 있는데
ay방향으로 만들어내고 있는데
회전자에 전류가 흐르고 있는데
아래쪽은 드가는 방향 위쪽은 나오는 방향으로 흐른다.
idl크로스b를 하면 T의 회전력이 발생한다.
T=mxB=an IS x ay By

an벡터를 y방향과 z방향을 나눠보면
파이가 90도 일때 최대 토크가 발생


전류방향을 바꿔줘야 같은방향으로 회전하게 됩니다.


가상의 이동을 이용해서 구하는것
constant flux
flux linkage가 변화가 없다. 변화가 없는 상태에서
dl만큼 circuit이 움직였다고 생각을 해봅시다.
flux linkage의 변화가 없기 때문에 소스가 외부에서 공급되지 않는다.
도체에 흐르는 전류가 이동을하면 일을 해주는것인데
그런데도 외부에서 에너지가 0라는것은
저장된 에너지가 줄어들든 늘어나든 한것이다
와이어가 움직였다=>운동에너지가 일을 해준것
에너지 관계로 힘 F를 구할 수 있다
가상으로 움직였다고 생각하면 그만큼 저장된 에너지가 줄어들었을 것이다.
dl만큼 이동을 했다=>Wm만큼 줄어들것이다.
저장된 에너지의 저장율을 구하게 되면 그쪽 방향으로 작용 힘이 된다는것
Ex.6-23

저장된 에너지의 힘에 의해서 아마추어가 움직였다고 생각해봅시다
dy만큼
저장된 에너지는 뮤가 무한대가 되면 자기회로의 저장된 에너지는 0가 됩니다.



위쪽 방향으로 힘이 작용한다는것을 알 수 있게 됩니다.
7장
Time-Varying Fields and Maxwell's Equations


E와 D, B와 H는 서로 분리되어있다.
전하가 시간에 대해서 변화하게되면
전류가 흘러들어오거나 나가는게 되는데
연속방정식에서

==>변화하는 성분에 대해서는 분리되 있지 않다.
변화하는 자기장은 변화하는 전기장을 만들어내고
변화하는 전기장은 변화하는 자기장을 만든다.
이 장에서 우리는 변화하는 자기장이
전기장으로 상승하거나 그 반대의 경우도 마찬가지입니다.
⇒ 두 쌍의 지배 방정식을 다음과 같이 수정해야합니다.
시변 케이스에서 전기장 벡터와 자기장 벡터 간의 상호 의존성을 보여줍니다.
⇒ 패러데이의 전자기 유도 법칙, Maxwell 방정식, 전자기파 전파
Faraday's Law

실험적으로 발표한 LAW 입니다.
시간에 따라서 변화하게 되면 폐루프에 전류가 유기가 된다.
시간에 따라서 증가를 시키면 전류가 유기가 된다.
와이에 전류가 흐른다는것
저항을 달아놓게 되면 저항에 의해서 제어되는 induced current가 된다.
자기장의 증가를 방해하는 방향으로 전류가 유기된다.
실험 법칙은 지금까지 해왔던데로 컬에관한 Equation을 가정하고 실험으로 발견한 법칙을 유도할 수 있어요
시간에 대해서 변화하는 자기장은 회전하는 전기장을 만들어 낸다.

Electric field는 이제 더 이상 보존장이 아니게 됩니다.
한항으로만 표현이 될 수 없다.
Electric field는 보존장이 아니다.
E=-∇V로 표현하기에는 부족하다.
변화하는 자기장으로부터 회전하는 전기장이 생긴다.
스톡스 정리를 하게 되면

면을 통과하는 자속의 변화하게 되면 그것에 의해서 회전하는 방향의 전기장이 발생한다.
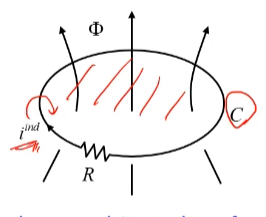
C라고 하는것은 와이어를 폐루프로 만들어서 C로해서 구성할수도 있고
가상의 폐루프를 생각을 해서 자기장이 시간에 대해서 변하게 되면
가상의 폐루프에 적분값이 0이 아닌것이라고 생각할 수 있다.

변화하지 않는 폐루프가 있을경우 미분항을 빼낼수가 있는데
자기장에 변화에 의해서 유기되는 기전력 emf

Lenz’s law
렌츠의 법칙:유기되는 전류에 의해서 자기장이 발생하게 되고 기존의 자기장을 방해하는 방향으로 생김
폐루프가 있고 자속이 위쪽 방향으로 향할 때
저항의 P2와 P1사이에 유기되는 기전력을 구하라!

V21은 C방향으로 적분한것
Ex. 7-1

r에 디펜던트합니다.
폐루프에 유기되는 기전력이 얼마인가
유기되는 기전력을 생각하면 파이를 먼저 구해야겠죠
파이라는것은 이중적분이죠?
회전하는 방향으로 균일하니까 2파이rdr로 적분해주면 된다~
적분이 cos(pi r/2b) ==>부분적분으로 구하게 되면 됩니다.
파이를 구할 수 있고 기전력을 구할 수 있다~
Transformer
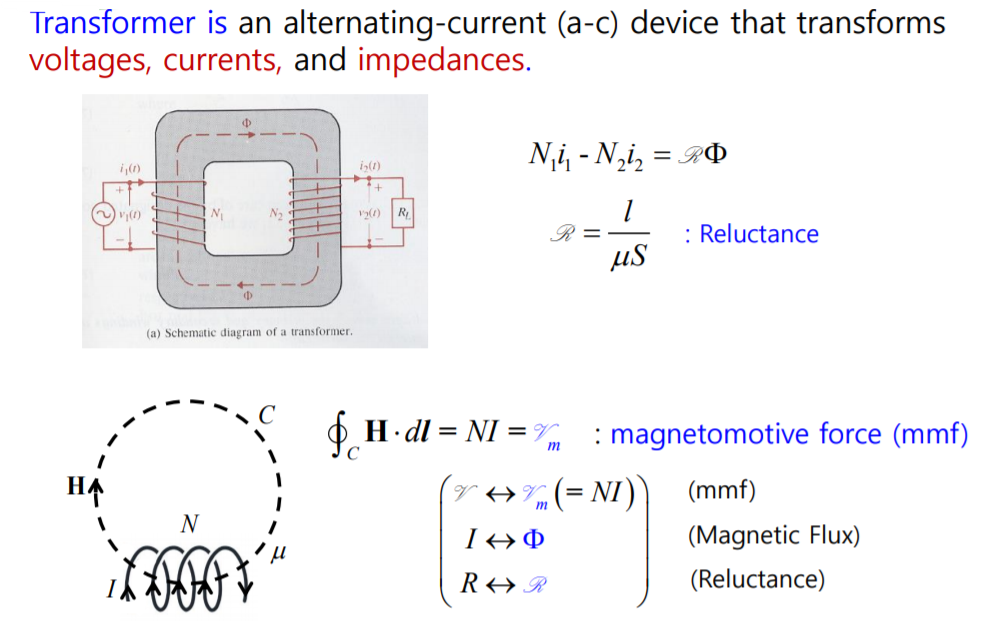
Transformer는 전력을 전송할 때 많이 사용하고
임피던스 변화를 할 때도 사용을 합니다.
전압을 높게하면 전류는 상대적으로
같은전력을 전송할때 흐르는 전류를 줄일수 있겠죠
고전압으로 바꾸어 줘야하는데
하이볼테지로 변환하고 다시 변전소에서 저전압으로 다시 바꿔주고 그러는것이죠
전압이 높아지면 전류가 낮아지게 되죠
임피던스 변환에도 사용된다.
1차 권선수를 N1 2차는 N2
1차측에 V를 가해서 전류 I가 흐르면
자속 파이가 발생하는데 코어를 통해서 파이가 지나가는데
뮤가 굉장히 높으면 1차측 자속=2차측 자속이 되서
내부저항이 0가 될겁니다.
그래서 이러한 형태에서 자기회로에 관한 식을 쓰게 되면
기자력

vm1-vm2=R파이
이렇게 됩니다. ==> 자기회로할 때 Ni를 vm으로 뒀었죠
리액턴스는 투자율S분에 1인데 뮤가 무한대가 되면 내부 리액턴스가 0가 되겠죠
Ideal Transformer

ideal할 때
뮤가 무한대==>i1/i2=N2/N1
반비례 관계가 있다.
전압의 비는 v1/v2=N1/N2
==>파이가 같기 때문입니다.
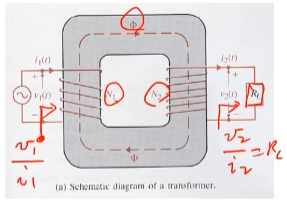
부하에 관한 변환관계를 생각해보기 위해서
2차측에 Rl이라는 부하가 관련이 있어요
식을 정리하면 임피던스는 권선수의 자승에 비례하게 된다.
==>부하 RL이 있을 경우에 임피던스를 변환을 할 수 있다.
예를 들면 스피커와 같은 것들..

엠플리파이어의 출력단이 임피던스는 높고
출력단의 임피던스와 스피커의 인풋 임피던스가 서로 매칭이 안되게 된다
==>트랜스포머를 달아서 증폭기의 출력과 매칭이 되도록 한다.
Real Transformer

뮤가 무한대로 가정했었는데 뮤가 무한대가 아니죠

누설이 없을 경우 v1,v2에 대해서 정리한것
2차측에 영향을 미치는것 까지 고려해줘야한다.
v1을 구할 때와 v2를 구할 때 파이가 같다고 하면 ==> leakage가 없는것인데
다르다면 leakage가 있는거겠죠? 그럼 상수k를 곱해줍니다.

리키지
인덕턴스
코일내부저항
뮤가 안에 있는 강자성체가 히스테릭시스
파워로스,eddy-current=>열손실
nonlinear core===> 위의 것들을 전부 고려해서 등가회로를 구해보면..

Xc:논 리니얼 현상
dot 코일의 방향에 따라서 위상이 달라질 수 있다.

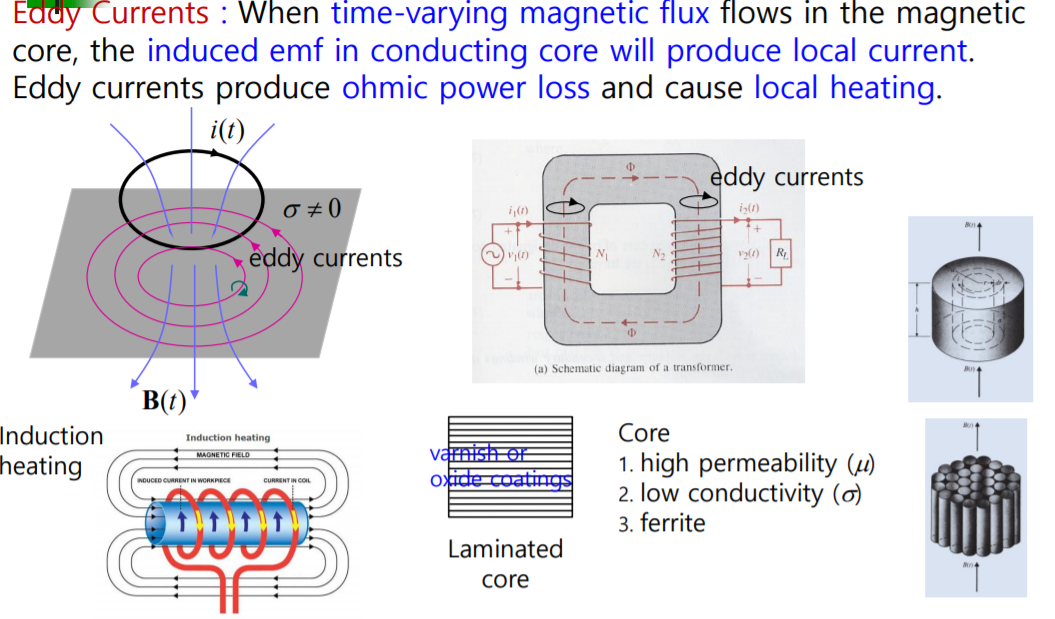
Eddy Current
자기장이 시간에 따라서 변화하게 되면 코어에 전류가 유기된다는것
강자성체가 있으면
그위에 도체를 해서 전류 I를 흘리면 자기장이 발생하게 되는데
자기장의 등가를 방해하는 방향으로 유기 기전력이 유기가 된다.
코어가 도체가 코어의 시그마가 0이 아니면 전류가 흐르지 않겠지만
0이 아니면 와류가 발생해서 ==>자기장의 방향을 방해하는 방향으로 발생
eddy current에 의해서 열이 나고 손실이 발생한다.
그래서 와류를 가급적 적게 하는게 좋겠죠

인덕션 히팅이라고 해서 와류를 적극적으로 활용하는것이 있는데
반대 방향으로 와류가 흘러서 도체가 실린더로 되어있는데
전류가 흘러서 열이 나게 되는겁니다.

코어에서는 줄여줘야 하는데
laminated core 철편을 이용해서 적층을 해서 코어를 만들어서
철편과 쳘편사이에 산화 코팅을 해서 전류를 흐르지 못하게 해서
와류의 흐름을 막는다.
A Moving Conductor in a Static Magnetic Field
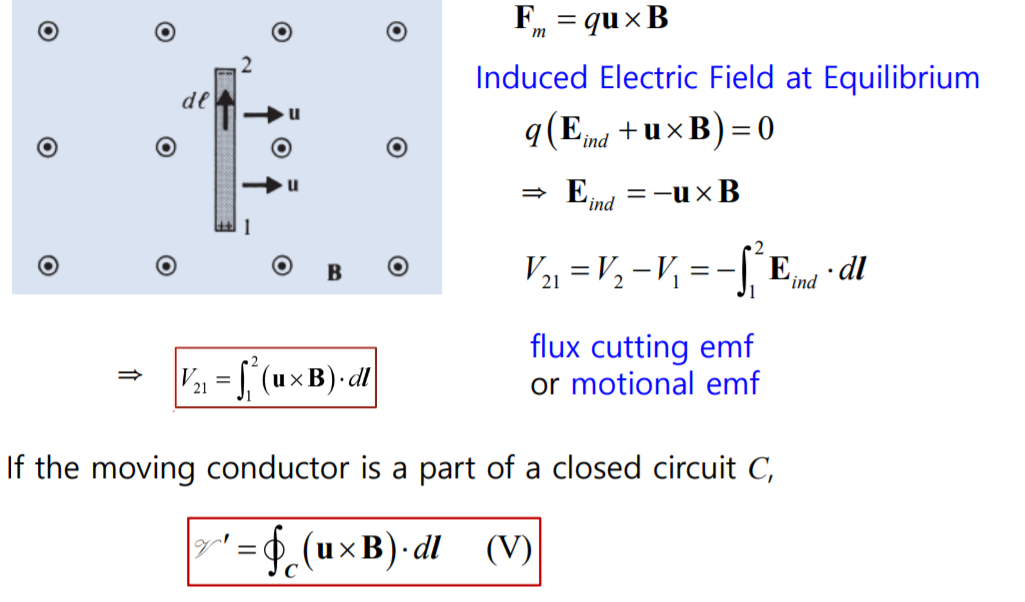
자기장 속에서 도체가 이동을 할 때
속도 u로 x방향으로 이동을 할 때
도체 내부에 케리어가 있는데
electron이 속도 u로 이동하게 되는데

힘을 받게 되겠죠?
두개 전하가 분리가 되서 무한히 멀어지지는 않을거에요==>다시 끌어다니는 힘이 작용하기 때문에
Equilibrium상태가 된다면?

발생한 전기장을 통해서 두 도체 사이에 발생한 기전력을 알 수 있다.

자기장은 static 도체가 지나가면서 flux cutting emf or motional emf라고 부름

도체를 걸쳐놔서 도체를 걸쳐놔서 속도 u로 x방향으로 이동을 시킨다고 해봅시다.
그럼 + - 기전력이 발생해서 전류가 흐르게 될것이다.
2번 프라임과 1번 프라임에 발생하는 전류를 계산해보면
u=ax방향으로 속도 u가 되고
-ay방향으로 ~~
전류는 +전압에서 I가 흐르게 되고 이러한 형태로 전류가 흐르게 됩니다.
흐르는 전류의 크기를 구해보면

저항에서 소모되는 전력은 얼마인가

내부에서 소모되는 전력을 구했어요==>일종의 발전기와 비슷한것이다.
이러한 전력은 어디서 발생하는가
저항에서 전력을 소모하게 되면 어디에선가 전력을 공급을 해줘야겠죠
==> 자기장이 가해지고 있는 상태에서 도체가 이동을 하고 있는데
도체를 만약에 이동을 하게 되면 저항이 연결되있지 않으면 전류가 흐르지 않죠?
기전력은 발생하지만 전류가 흐르지 않아서 힘을 받지 않게 됩니다. 도체는
저항을 연결하면 전류가 흐르게 되고

마그네틱 포스가 작용하게 됩니다.
기계적으로 x방향으로 힘을 가해줘야 뮤로 이동할 수 있다.
자기장이 가해지고 있는데 도체를 속도 u로 이동하게 되면
아무런 문제가 없어요
저항을 달아서 전류가 흐르게 되면 저항에서 전력소모가 일어난다
그렇다면 전류가 흘러서 외부에서 힘을 가해줘야 전력을 소모할 수 있다.
저항에서 소모되는 전력만큼 기계적으로 전력 소모가 해당되는 양만큼 기계적으로 힘을 가해줘야
한다는것을 보여줍시다.
파워는 에너지의 단위시간당 공급되는 에너지가 됩니다.
미소 길이 이동하는데 한 일의 양 F.dl이 되겟죠
시간에 대해서 미분을 해주게 됩니다.
기계적 파워는 F.u가 됩니다.
마그네틱 포스와 미케니컬 포스는 같다!


발전기를 돌릴때 부하를 달아서 소모가 된다면 힘이 굉장히 들것이다.
부하를 달지 않으면 기전력은 발생하지만 실제 전력소모는 일어나지 않죠
하지만 부하를 달게 되면 전류가 흘러서 전력소모가 일어나면서
회전하는 방향의 반대방향으로 힘이 들게 됩니다. 그만큼의 힘을 더 가해줘야한다.
Ex. 7-3 Faraday disk generator

기전력이 발생한다.
어떻게 발생하는가=> 판이 회전하지만 가상의 선을 생각했을 때
선이 판이 회전을 하고 있으니 속도 u로 회전을 하고 있을거야
이 선이 속도u로 회전을 하게 되니 u x B에 해당하는 기전력이 발생하게 된다.
가상의 선에 발생하는 기전력을 생각해봅시다. 3~4번 까지 u x B를 적분해주면 됩니다
2번과 1번 사이에 기전력이 발생하게 됩니다.

두가지 이야기를 했는데 루프가 가만히 있는 상태에서 자기장이 변화하면 기전력이 유기된다.
자기장이 static인 상태에서 와이어가 이동하면 기전력이 유기된다.
시간에 대해서 변화하는 자기장이 있는데
도체가 이동할 경우 생각을 해보도록 합시다.
두 힘을 합치게 되면

오른쪽은 도체가 이동을해서 생성되는 기전력 u x B에 해당되는 두가지 전기장에 의해서 힘을 받게 됩니다.
두개 합친것이 도체에 작용하는 전기장이 된다!!!
내부에 발생하는 전기장을 적분한 양은 어떻게 되느냐?
결과적으로 전기장은 자기장의 변화에 의해서 발생하는 전기장 + 와이어 이동에 의한 전기장
패러데이 법칙의 general form

왼쪽항은 변화하는 자기장 내에서 발생하는 기전력에 대한것
두번째항은 motional emf

두가지 성분을 다 고려한 성분의 변화율에 해당하는것으로 생각해 볼 수 있겠죠
d파이/dt 자기장의 와이어가 변화해서 발생하는 기전력
우리가 아까 두항으로 썼지만 자기장의 변화와 루프의 면적의 변화를 고려해서 시간에 대해서
미분한것이 기전력과 같다는것을 확인해보려합니다.

t인 순간에 C1이 있다.
C2로 이동할 때 그럴 경우에
C를 통과하는 자속의 변화율을
B도 변화 s도 변화하는 것을 전체적으로 계산해 보라
델타 t분에 각값을 빼주면 미분이 되겠죠
t에 자승이상의 오더를 해서 무시를 할 수있겠죠
두개의 항으로 나눌 수 있겠죠


-를 붙인것이 emf가 되니까

자기장의 변화와 면적의 변화를 다 합쳐서 d파이 dt로 해주면 된다.


도체를 통과하는 자속 파이를 구해서 기전력을 구할 수 있다.



변화하는 자기장 내에서 폐루프가 이동할때 발생하는 emf를 구하는 식을 쓰는데
자기장의 변화에 의한 성분
루프가 이동할 때 발생하는 성분이 더한것이
전체 루프안에를 통과하는 디파이 오브 디티의 식으로
표현할 수 있다는것을 적분식으로 써서 제출하세용

'RF 시스템 설계 > 전자기학II' 카테고리의 다른 글
| Time-Harmonic Fields (0) | 2020.10.04 |
|---|---|
| Maxwell's Equations & Wave Equations (0) | 2020.09.26 |
| Inductances and Inductors (0) | 2020.09.07 |
| Boundary Conditions for Magnetostatic Field (0) | 2020.09.07 |
| Poisson's Eq 풀이를 위한 중요 개념 정리 (0) | 2020.09.03 |