
Capacitor

충전되는 전하량은 가해준 전압에 비례한다.
그 비례상수 파라미터를 C로 정의한다.
전기장 안에 전기 에너지가 저장이 되서 전기에너지를 저장할 수 있는 소자
Inductor

전류 I가 흐를 때 자기장이 발생하겠죠
자기장이 폐루프 C를 통과해서 지나가는것을
링크하는 flux라고 합니다.
I에 의해 발생하는 발생하는 자기장 중에서
면을 통과하는 자속
단면적 S를 통과하는flux가 링크하는 flux가 되니까
자기장 B가 회로를 링크하는 자기장인데
자기장의 총 flux를 자속이라고 한다.
파이는 전류에 비례하게 된다.
비는 전류에 비례하잖아요.
I하고 파이는 서로 비례하는 양이 됩니다.
폐회로에 전류 I를 흘렸을 경우
폐회로를 통과하는 자속이 발생하게 되는데
자속하고 전류 사이에 비례상수 비례관계에
인덕턴스라고 정의를 하겠다.
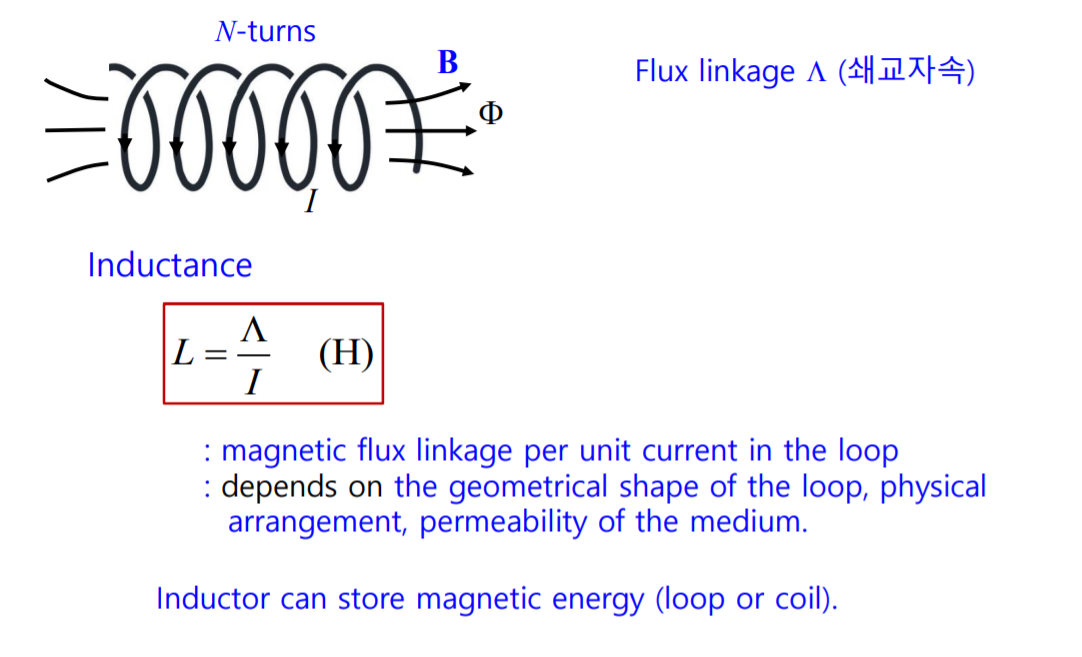
폐루프가 한바퀴만 감았을 경우에
파이하고 I 사이의 비를 비교를 했었는데
링크하는것은 N배로 늘어나게 된다.
이것을 쇄교자속이라고 한다.
Flux linkage
램다가 링크하는 flux가 된다.
인덕턴스는 쇄교자속을 I로 나눈것이다.
N번 링크한것이 왜 중요하냐면
자기장이 통과하게 되면 기전력이 발생하게되는데
쇄교자속과 연관이 있다는 말이야
쇄교자속을 전류로 나눈것이야.
루프의 형태, 모양이라던지 permeability 등등에 따라서
결정이 됩니다. 자기장이 형성되서
magnetic energy를 저장이 됩니다.
Self inductance

인덕터가 있으면 인턱턴스를 구하는 순서
전류로부터 자기장을 구하고
앙페르 주회법칙 혹은 비오사바르를 적용해서
==>B를 적분하면 파이가 되고
파이에 권선수가 있으면 N을 곱해서 램다를 구해서
인덕턴스를 구할 수 있다.
Mutual Inductance

C1에 I1을 흘려주게 되면 자기장이 발생하겠죠
B1이 발생하게 되는데 B1중에 S1을 통과하는 양에 의해서
self inductance를 결정할 수 있었는데
B1중에 일부가 S2를 통과하는 양을
Φ12라고 얘기하는데 B1을 s2에 대해서 적분하면
Φ12가 됩니다.
I1에 비례하는 값이 될거에요.
I1에 대해서 얼마만큼의 Φ가 발생하는지를 나타내주는것을
상호인덕턴스'라고 부릅니다.
Flux linkage L12

I1에 의해서 B1이 발생하고
B1의 일부가 C2를 통과하게 되면 Φ12가 됩니다.
만약에 C2가 권선수가 N2번 감겨져있으면
쇄교자석이 램다를 구해줘야겠죠
I1과 램다 사이에서 L12를 구할 수 있겠죠
C1에 흐르는 전류 분에
C2를 통과하는 flux linkage 쇄교자속이라고 얘기할 수 있겠죠
Neumann formula

Magnetic Energy

인덕터에 전류 I가 흐를 경우 에너지가 얼마나 저장되느냐?
인덕터에 전류가 0에서부터 흐르기 시작하면 기전력이 발생
전류의 증가에 비례하는 기전력이 발생하게 되는데
자속의 증가에 비례하는
패러데이 법칙에 의해서 전압이 발생
전류의 흐름을 제어하게 되어서
전류가 변화하면 전류의 변화율에 비례하는 전압이 발생하고
전압에 의해서 흐르는 전류를 제어한다.
전류의 변화율이 점점 줄어들어 양단 전압이 줄어들고
전류는 최종적으로 최대로 흐르고
저항 아래 모든 전압이 걸린다.
전압은 점점 줄어들게 된다.
전원으로부터 인덕터로 흘러들어가는
전력=iv
전류가 i로 흐르는 동안에 인덕터에 자기 에너지가 저장되어있다.
장내에 에너지가 저장되는것
Magnetic energy에 해당하는 일을 해줘서
인덕터에 magnetic energy가 저장된다.
인덕터 양단의 전압=Ldi/dt

두 회로가 분리되어있다면
W1=(1/2)L1I1^2
상호인덕턴스에 의한 에너지도 구해야됨
v21:C1에 유기되는 기전력
v21이 유기가 되는데 대문자 I1이라는 전류가 흘러서
에너지가 저장되는것
W2=1/2)+L2I2^2
W1+W21+W2 더한것이 전체 인덕턴스에 저장된 에너지다.


E와 D로 표현이 가능하다
field의 양으로 표현해보자
k번째 루프
굵은 컨덕터에 전류 I가 흐른다고 생각해보자
필라멘트들이 모여서 Ck의 와이어가 된다고 생각하면
k번 째 루프를 통과하는 파이케이를 생각하면
B라는 것은 컬A==>스톡스의 정리로 변환
파이케이를 다시 쓰게 되면 integral 이런 식으로 쓸 수 있다.
하나의 루프가 굵다고 했죠
각각의 필라멘트에 저장된 에너지를 더해주면 된다고 했죠
k번째 와이어 안에 전체 k번째 와이어를 구성한다고 생각해보면
각각의 필라멘트의 루프에 해당하는 필라멘트를 곱해서 k번째 루프에 저장되있는 에너지가 된다.
루프가 하나만 있다.
루프가 굵어서 N개의 필라멘트로 구성되어있으면
N개의 필라멘트로 구성된 에너지가 얼마냐

R을 무한대로 보냈을 때
A는 포텐셜 함수이므로 1/R 에 비례한다.
H는 1/R^2에 비례
두번째 항은 무한대로 확장하면 0으로 가고 첫번째 항만 남는다.

(1/2)LI^2
field가 분포하는 영역안에 1/2H·B에 해당하는 에너지를 전부 적분하면 위와 같은 식이 된다.
Flux linkage를 적분해서 L을 구할 수도 있고

위와 같은 방법으로 구할 수도 있다.

hole이 캐리어가 되면 방향이 바뀐다.
기전력이 -가 발생할것이다.
Magnetic Forces and Torques

와이어에 전류가 흐를 때
그 전류가 흐르는 와이어가 자기장 내에서 힘을 받게 되겠죠
와이어 중에 dl의 방향은 전류의 방향과 같아요.
dl이라는 매우 짧은 도선의 일부를 생각해보면
도선에 들어있는
electron들이 받는 힘에 대해서 생각해보죠
총 전하량이 속도 u로 이동할 때
-NeSdl: 전하량 q
u는 electron의 방향입니다
전류랑은 반대방향이라서 절대치를 u에 붙입니다.
전류 I는 electron이 있으면
여기에 단면적 S를 하고 u의 절대치를 하면 전류 I가 된다.
미소길이에 전류 I가 흐르고 있을 때
Idl x B로 dFm을 표현 가능하다.

'RF 시스템 설계 > 전자기학II' 카테고리의 다른 글
| Maxwell's Equations & Wave Equations (0) | 2020.09.26 |
|---|---|
| Manetic Torques & Time-Varying Fields and Maxwell’sEquations (0) | 2020.09.19 |
| Boundary Conditions for Magnetostatic Field (0) | 2020.09.07 |
| Poisson's Eq 풀이를 위한 중요 개념 정리 (0) | 2020.09.03 |
| 정전기장 정자기장 복습 [이택경 교수님 강의 6-4,6-3 정리] (0) | 2020.09.03 |
