


r=0일 때 마지막 서클 r이 무한대 일때는 오른쪽 점이 될것이다.
x=0일 때 중간의 빨간선이 될것이고 x가 +이면 위의 선
무한대가 되면 오른쪽 점
왼쪽점은 쇼트
오른쪽점은 오픈
중간에 있는 점은 Rl=R0일 때
즉, reflection 계수가 0일 때
위쪽은 리액턴스가 0보다 커서 인덕티브
아래쪽은 리액턴스가 0보다 작어서 캐패시티브
파란색 선은 Rl<R0일 때 빨간색선은 Rl>R0일 때


부하로부터 전원쪽으로 이동하면 감마의 크기는 일정하고 스탠딩웨이브 레이시오도 일정하다
Zl이 있을 때 S값이 얼마인가? 전원쪽으로 이동하다가 전압이 최대가 되는 지점 PM에서 r>1인데
PM지점에서 인풋임피던스가 저항성분이 되고 r값(노멀라이즈드 저항)이 즉 S값이 된다.
r값이 즉 S값이 된다. 소문자 pm지점에서는 전압이 미니멈이 된다. 어떤 S를 구하라 하면 PM지점에서 r을 읽으면 된다.
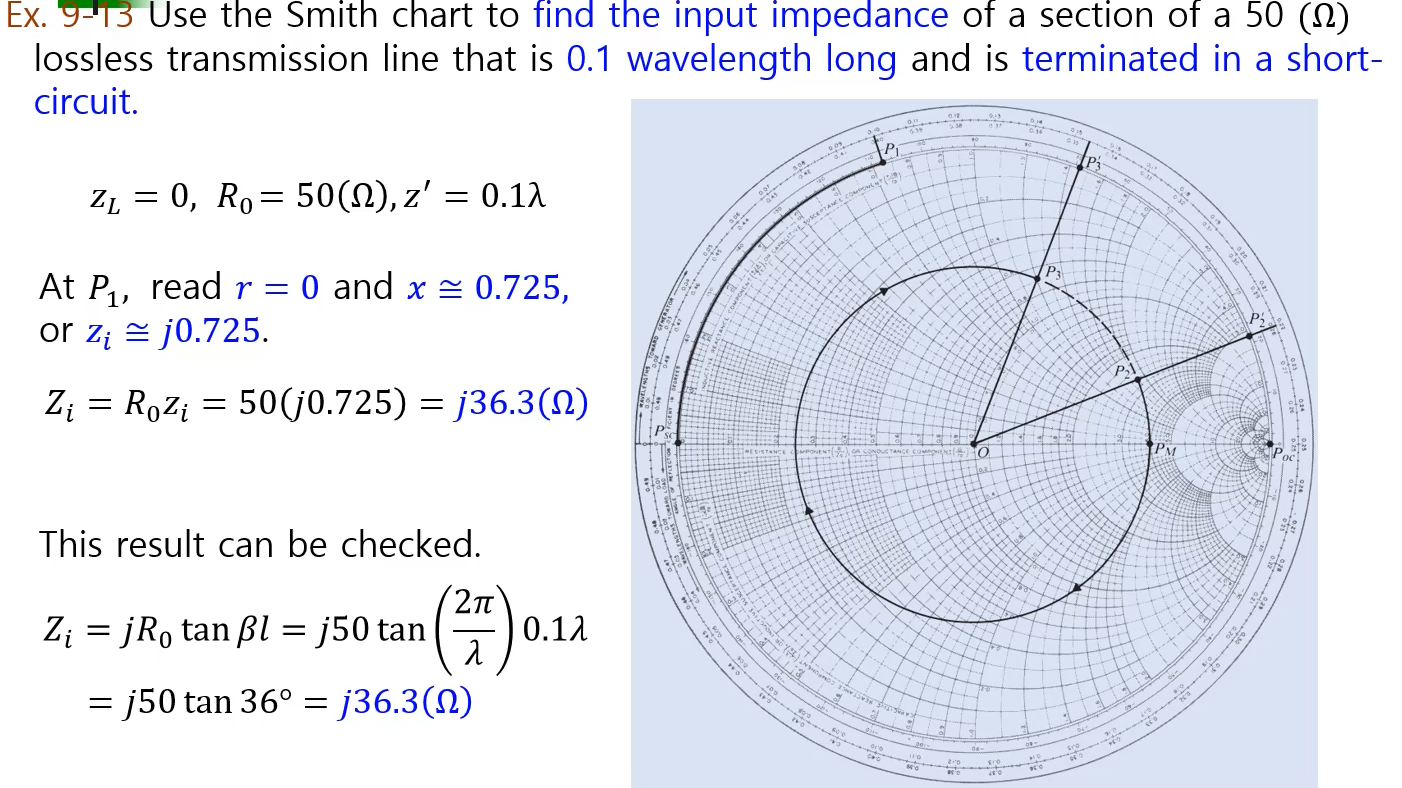

부하가 260+j180 옴 R0가 100옴
나머지를 구하라 반사계수를 구하라 하면 부하지점에 P2지점의 부하를 구해서
이 지점의 감마의 크기를 구해준다. 세타T를 구하라 각도 사이의 파장의 길이*4pi 하면 구할 수 있고
스탠딩웨이브 레이시오는 PM지점의 r값을 읽으면 된다.

인풋임피던스는 얼마인가
0.434램다만큼 회전시켜서 P3로 가야한다.
이때 r값과 x값을 읽어서 zi를 읽는다
전압 맥시멈은 PM지점에서 읽으면 된다.


예제 9-9를 차트를 이용해서 구하는 문제가 되겠습니다.
선로의 스탠딩웨이브 레이시오가 3.0일 때 전압을 측정하니까 부하로부터
미니멈 포인트가 나타나는데 z'm이 0.05m 일때 Zl을 구하라
lm'과 Rm'으로 가상의 선로로 연장해서 여기서 들여다본 인풋임피던스를 구해서 Zl을 구하는 방법
두번째는 감마를 계산으로 구해서 S로부터 감마의 크기를 구하고 Zm'으로 세타T를 구해서 Zl을 구할수 있었다.
이번에는 차트가 주어져있고 S가 주어져 있으니까 S로부터 감마를 구하고 Zl을 구하라
a) S 로부터 감마를 구하라
S=3이면 PM 지점에서 r=3인 서클인 지점을 찾으면 된다.
PM지점을 이용해서 감마의 크기를 구한다.
b)ZL을 구하라
차트상에서 ZL을 구하기 위해서는 미니멈 포인트를 알고 있다
소문자 Pm지점에서 Zm'지점이 되는데 Z'이 0이 되는 지점이 어디인가
Zm'으로부터 부하쪽으로 이동해야한다. 0.05/0.4 즉 0.125 wavelength toward 이동한다
0.125램다 만큼 이동을 한다. 그지점이 부하지점이 된다.
Zl값을 읽으면 됩니다. r값을 읽으면 0.6 x값도 읽어주고
zl=0.6-j0.8 여기에 50옴을 곱하면 ZL을 구할 수 있다.

lm'과 Rm을 구하라
람다/2=0.2m
zm'은 0.05m
Rm은 R0/S = 16/7 옴
차트를 이용해서 구해보자

차트에서 선로가 로스가 있을 때 어떻게 되느냐?
로스가 어느정도 적은 경우에 생각해보자
선로의 로스가 있으면 알파가 0이 아니다.
감마의 크기는 e-2Az로 줄어들게 된다
부하의 위치에 회전을 하게 되는데 인풋임피던스의 크기가
인풋지점의 감마의 크기가 익스포넨셜로 줄어든다.
감마 위치를 정확하게 찍으면 된다.
책에서는 z를 이야기 하는데 감마를 정확히 알면 z를 읽어주면 된다.

로드가 쇼트일 경우에 쇼트로부터 2m 이동했을 때
인풋 임피던스를 재보니까 45+j25 이럴 경우에 알파와 베타를 구하라
P1 지점 인풋임피던스가 0.6+j3.0 (쇼트로부터 2m 이동한 지점)
알파값이 0이 아니여서 감마가 줄어든다 ==0.89=e-2al 알파를 구할 수 있다.

베타는 2m가 0.2 웨이브 length
람다는 2/0.2==>10m

알파와 베타를 구하면 똑같이 웨이브 랭스만큼 회전한다음
알파만큼 곱해서 인풋임피던스를 로시한 경우에도 구할 수 있다.
로시한 경우에는 알파를 감안해서 곱해주면 된다.


임피던스 매칭은 부하임피던스를 특성임피던스와 같아지게 하는것이다.
결국은 스탠딩 웨이브 레이시오가 최소가 되도록 1이되도록 해줘야 하는데
최대 전력을 부하로 전달하기 위함이다.
리프렉션이 있으면 신호를 왜곡시킬수 있다. 그래서 그러한것을 막기 위해서 임피던스 매칭을 시킨다.
첫번째 방법은 quarter-wave transform을 이용하는 방법

λ/4 선로를 이용하면 인풋임피던스 = R0^2/ZL 되서 ZL에 반비례하게 됨
RL이 있고 R0에 매칭 시킬 때

들여다본 인풋 임피던스가 R0'^2/RL 이 성립하는데
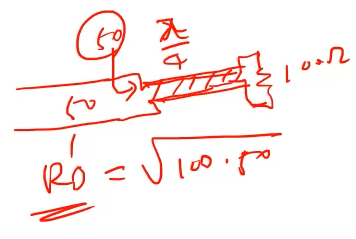
R'0값을 조정하면 임피던스 매칭이 된다.
부하가 컴플렉스면 RL이 복소수가 되고 R0'이 컴플렉스가 되서
로시 라인이 된다==>정확하게 매칭시키는게 힘들다, 주파수에 민감하다
하지만 완벽하게 임피던스 매칭을 시킬 필요는 없다.

동일한 전력을 공급하고 싶다.
각각의 인풋 임피던스가 같아야 한다.
R01'과 R02'에는 스탠딩 웨이브가 발생한다.

r과 x에 관한 차트를 그려서 생각했는데==>임피던스 차트
이제는 어드미턴스 차트를 생각해봅시다.
임피던스의 역수로 볼 수 있다.
정규화된 어드미턴스는 G0로 나눠주면 된다.
yl=g(컨덕턴스)+b(서셉턴스)
yL을 임피던스로 써보면 zL의 역수가 되는것을 알 수 있다.
스미스 차트에서 yl가 zL 관계
인풋임피던스가 ZL의 역수가 된다.






stub를 이용하는 방법은 부하가 임피던스가 리얼이 아니여도 된다.
임의의 부하 임피던스에 대해서 매칭 시킨다.
부하로부터 d만큼 이동해서 쇼트 스터브를 parallel로 연결한것을 shunt-short stub라고 부른다.
shunt-open stub 션트 스토브는 구현하기 용이하다.
오픈 혹은 쇼트하게 되면 리액턴스나 캐패시턴스로 동작한다.
R0의 매칭을 시키기 위해서 들여다본 임피던스가 R0가 되어야 한다.
ZL로부터 길이d만큼 오다보면 인풋임피던스 리얼파트가 R0 되는 위치가 있다.
또는 노말라이즈드 임피던스가 1이되는 위치에서 멈춘다음 병렬로 리액턴스를 달아줘서 매칭시키는 방법이다.
d와 길이 l을 얼마로 하면 되겠느냐가 shunt stub의 문제

ZL로부터 YL을 구하면 어드미턴스 차트가 되겠다.
d만큼 제너레이터 쪽으로 이동하면 g=1인 서클을 만나게 된다.
솔루션이 두개가 있다. d1, d2
d만큼 갔을 때 yb 포인트



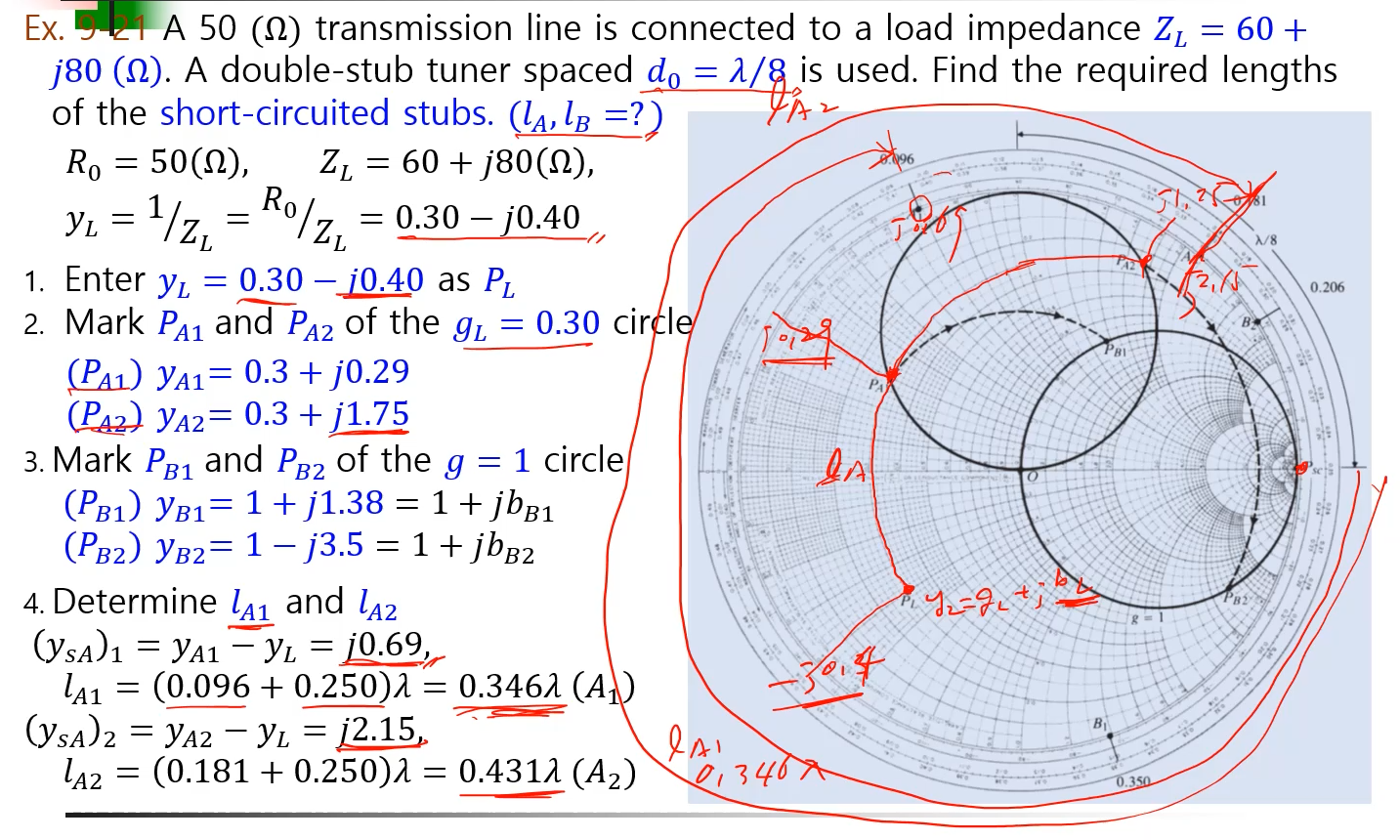
예제9-20
싱글 스토브에서 오픈스토브를 사용했을 경우 d와 lb 둘중 하나 구해서 제출

d0를 고정시킨다. 이렇게 하는 이유는 회로 설계할 때 스토브의 크기를 원하는 길이로 픽스 해두고
회로를 구현하겠다는 의미이다. d0를 정해놓고 원하는 스페이스에 넣어주는것 입니다.
B-B'에서는 싱글 스토브랑 비슷
d0만큼 이동해서 부하에서 매칭해줘야한다.
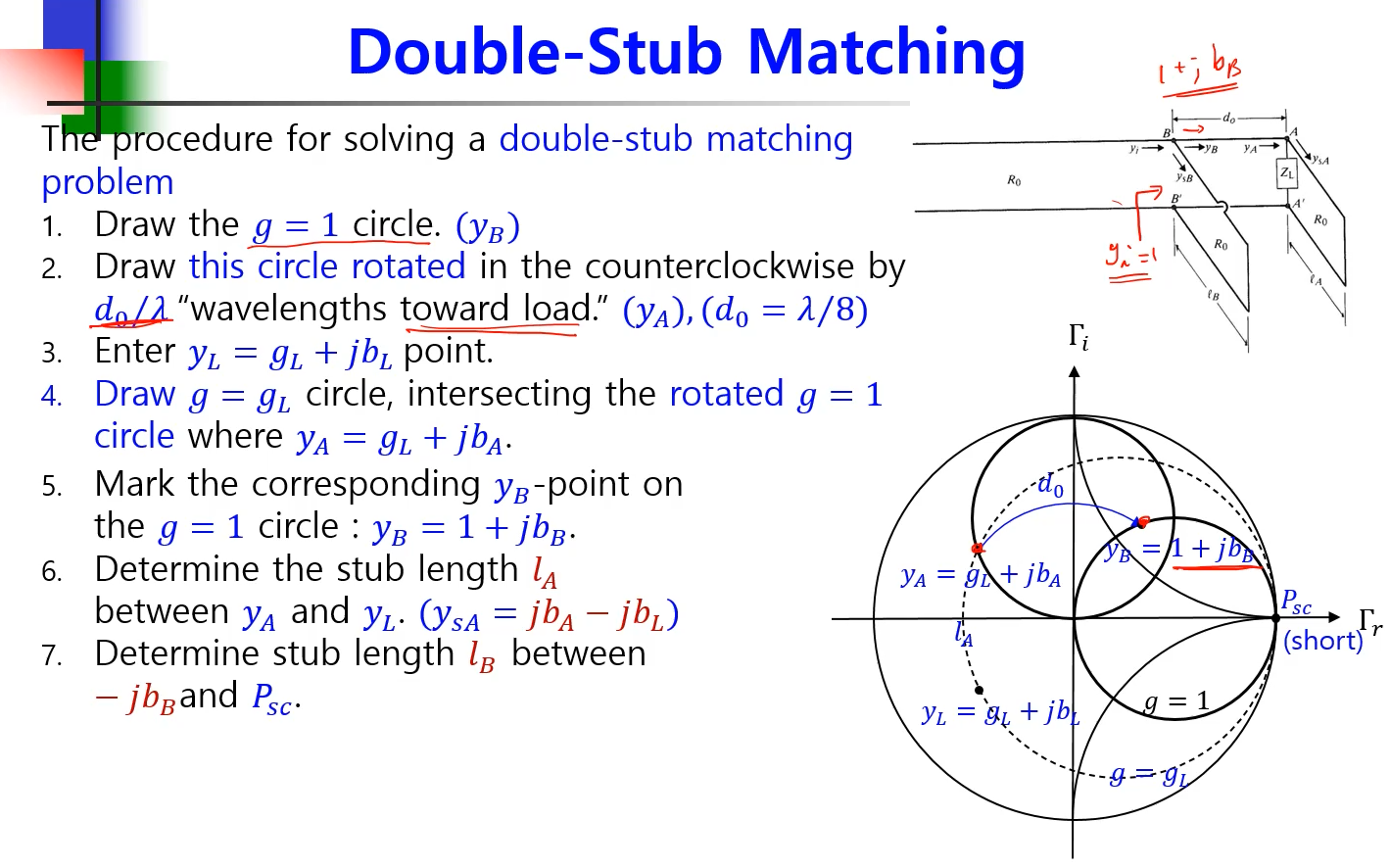
d0/λ 만큼 회전한 서클을 만들어준다.
더블 스토브는 서셉턴스 차이에 해당하는 la 부분만 신경써주면 됩니다.


完
'RF 시스템 설계 > 전자기학II' 카테고리의 다른 글
| 전자기학II [평면파~전송선로 이론][8장~9장 정리] [完] (0) | 2020.12.16 |
|---|---|
| Transients on Transmission Lines (0) | 2020.11.29 |
| Finite Transmission Lines (0) | 2020.11.22 |
| Transmission Lines (1) | 2020.11.14 |
| Oblique Incidence at a Dielectric Boundary (0) | 2020.11.06 |
