


지난주에 부하가 특성임피던스와 다를경우 인풋임피던스가 위치에 따라서 어떻게 달라지는지
트랜스미션의 쇼트나 오픈을 통해서 LC를 구현할수있고 쿼터웨이브
저항성분일 경우에 전압이 최대 혹은 최소 이렇게 생각을 했고
임의의 부하가 있을 경우 트랜스미션 라인에 스탠딩 웨이브를 봤었고
전원이 매칭되지 않았을 경우 전원쪽에서도 반사가 일어나니까 전압 전류가
무한급수로 나타난다는 얘기를 했었다.

선로를 이용해서 펄스를 만드는 방법 스미스차트에 관한 얘기를 하겠다.


볼테지나 커런트를 표현할 때 페이저를 이용해서 표현을 했었고
리액턴스x 웨이브랭스, 웨이브넘버, 페이즈컨스턴트 등등 얘기 했었는데
transient에서는 싱글 프리퀀시가 아니여서 위의 값들을 얘기하면 안된다.
의미가 없는 값들이 된다. 컴퓨터의 펄스 디지털 시그널 파워라인의 서지 문제
디지털신호를 가하게 되면 회로이론대로 디지털 신호로 값이 나타나는줄 알지만
알수없는 에러같은것들이 전송선로에서 과도현상문제를 잘 생각해봐야한다.
주파수가 높아지게 되면 이 과도현상이 심각한 문제를 발생시킬수 있다.
임피던스 매칭을 해야 특별한 문제가 발생하지 않는다.

transient일 경우에도 특성 임피던스 R0는 유효한 값이 됩니다.
속도도 마찬가지로 유효한 값이 됩니다.
만약에 선로의 터미네이션이 L이나C가 되면 펄스상태로 반사가 되지 않아서
미분방정식을 풀어서 어떻게 과도현상이 나타나는지 풀어줘야 한다.
부하가 연결되었을 때, LC가 있을 때 과도 현상을 살펴보자

V0가 있고 Rg가 있고
특성임피던스와 같은 부하가 연결되어있다고 보자=>좀 쉬운 문제가 될것
t=0일 때 스위치를 닫으면
전원에서 볼때 Time harmonic에서 steady state일 경우에
신호가 한참 가해진 후에 시간이 지나서 부하의 영향이 전원의 입구에서 영향을 미친다.
하지만 스위치를 닫는 순간에는 부하가 무엇이 연결되어있는지 모른다.
R0만 연결되있는것으로 보게 된다.
Rg와 R0가 연결되있는것으로 전원은 인식을 하게 된다.

이 신호가 오른쪽으로 트레블링을 하게 됩니다.
V1+가 가해져서 오른쪽으로 이동하게 된다.
이동을 하다가 부하에 도달하면 임피던스가 매칭되있어서 반사가 일어나지 않는다.
t=l/u이 될 때까지 과도문제만 발생한다.
이전에는 일부분 전압이 나타나고 일부분은 나타나지 않게 된다.
시간축에서 볼 때도 처음에는 전압이 나타나지 않다가

나타나게 되고 반사가 일어나지 않기 때문에 계속해서 V1+가 나타나게 됩니다.
전류는 V1+/R0가 될것이다.
부하가 매칭되어있기 때문에 타임딜레이가 나타난 이후에 전압이 나타난다.

부하가 매칭되있지 않은 경우를 보도록 합시다.
스위치를 닫으면 V1+가 발생을 하게 됩니다.
그러다가 t가 l/u이 되게 되면 감마L이 0이 아니여서 반사가 일어나게 됩니다.
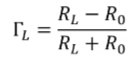
Rl이 R0보다 클 때

왼쪽으로 이동하게 됩니다.
t가 2T가 되면 또다시 반사가 일어나게 되겠죠
감마g도 존재한다. 다시 반사가 일어난다.

V2+가 일어나게 된다.
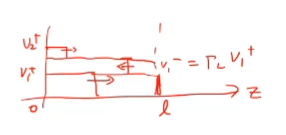
계속해서 반사를 합니다. 감마가 1보다 작은 값이어서 결국에는 수렴하게 됩니다.
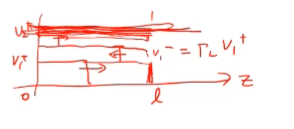
계속해서 transient가 발생하게 되는것 입니다.
전압이 계속 변해가다가 어떤 값으로 수렴하게 됩니다.
타임에 대한것 포지션에 관한것을 생각하게 되지만
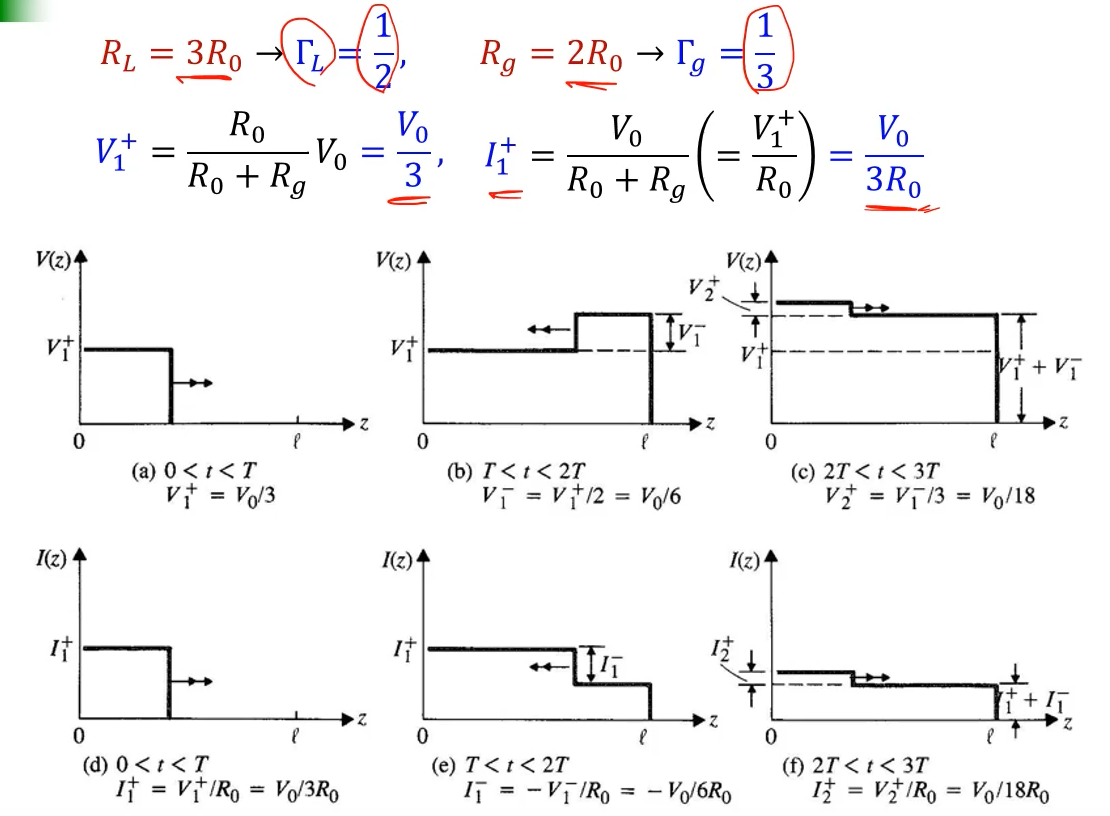
전류에 대해서는 반사계수의 부호를 마이너스를 붙여줘야 한다.
I2+=TgI-===> +값이 된다.

주의해야할 두가지 점이 있다.
감마l과 감마g는 +가 될수도 있고 -될수도 있다
감마l과 감마g는 1보다 작다.
능동소자에서는 오실레이션할 수 있도록 1보다 더 큰값을 발생시킬수 있지만
수동 소자에서는 감마값이 1보다 작게 된다.==>특정값으로 수렴하게 된다.
부하도 매칭안되있고 전원도 매칭되있지 않을때
부하에 나타난 전압은 시간이 한참 지나면 전압들이 계속 누적이 된다.
반사계수가 계속 곱해져서 더해진다.
건너뛰어서 한 항을 만들어내게 되고 감마L을 곱해준 다음에 한항을 만들어 줄수 있다
이 값들이 등비급수가 되어서 결과적으로 파란색 식이 된다.

대입해봤을 때

스위치를 닫으면 왔다갔다 하면서 트랜지션이 발생하고
선로가 작으면 2R0와 3R0가 전압 분배가 일어난것 처럼 된다.
DC의 전압분배와 비슷하게 수렴하게 된다.
우리가 주목하는것은 트랜지언트 과정
전압이 계속 변화하는 과정이다
펄스 주파수가 높아지고 선로의 길이가 길어졌을 때
트랜지언트 문제가 중요한 문제가 될것이다.
전류도 마찬가지로 모든 성분을 더해보면
반사계수가 -가 된다. 부호가 +-+- 바뀌게 된다
1-감마L로 바뀌게 된다.
최종적으로 V0/5R0
과정에서 t만큼 트랜지언트가 계속 일어나서 수렴하게 되지만
트랜지언트가 존재한다.

특정지점에서 시간이 증가함에 따라서 전압이 어떻게 변하는지 특정시간에 선로상의 전압의 분포를
잘 생각해보면 알수있겠지만 어려운문제이기에 좀 더 쉽게 풀기 위해서 리프렉션 다이어그램을 이용한다.

시간이 증가함에 따라서 위치가 이동하게 되는데 시간과 위치를 다이어그램으로 그려보도록 하자.
t가 증가할 수록 z가 오른쪽으로 이동하게 된다.
V1+의 위치는 시간이 증가함에 따라서 z도 같이 이동하게 된다.
t가 대문자 T가 되었을 때 l에 도달하고 l에 도달하면 V1+는 반사가 일어나고
2T가 되면 감마g가 곱해져서 이동을하고 4T가 되면 다시 감마g가 곱해져서 반사가 일어난다.
V1+가 도달하기 이전 전압이 나타나지 안혹 V1+가 도달하면 V1+가 일어나고
T에서 반사가 일어나면 V1+와 V1-가 일어나고 이런식으로 각각의 영영에서 전압이 나타난다.

0에서부터 t1에 도달하기 까지는 전압이 0 그담에는 V1+ ~~ 각각의 시간의 범위에 따라서 각각의
전압이 다르게 나타나는것을 확인할 수 있다.
선을 그어서 선 상에서 전압이 변화하는것을 그릴 수 있다.
reflection diagram을 이용하면 선로의 transient 문제를 쉽게 풀수 있다.

전류에 대해서도 알아보자

전원이 펄스가 발생했을 경우 어떻게 나타날까
유닛 스탭 function을 정의한다. u(t)
펄스는 중첩해서 표현해줄수 있다.
이러한 신호가 가해졌을 때 트렌지언트는 어떻게 되겠는가

합쳐지면서 0가 되는 구간이 존재한다.
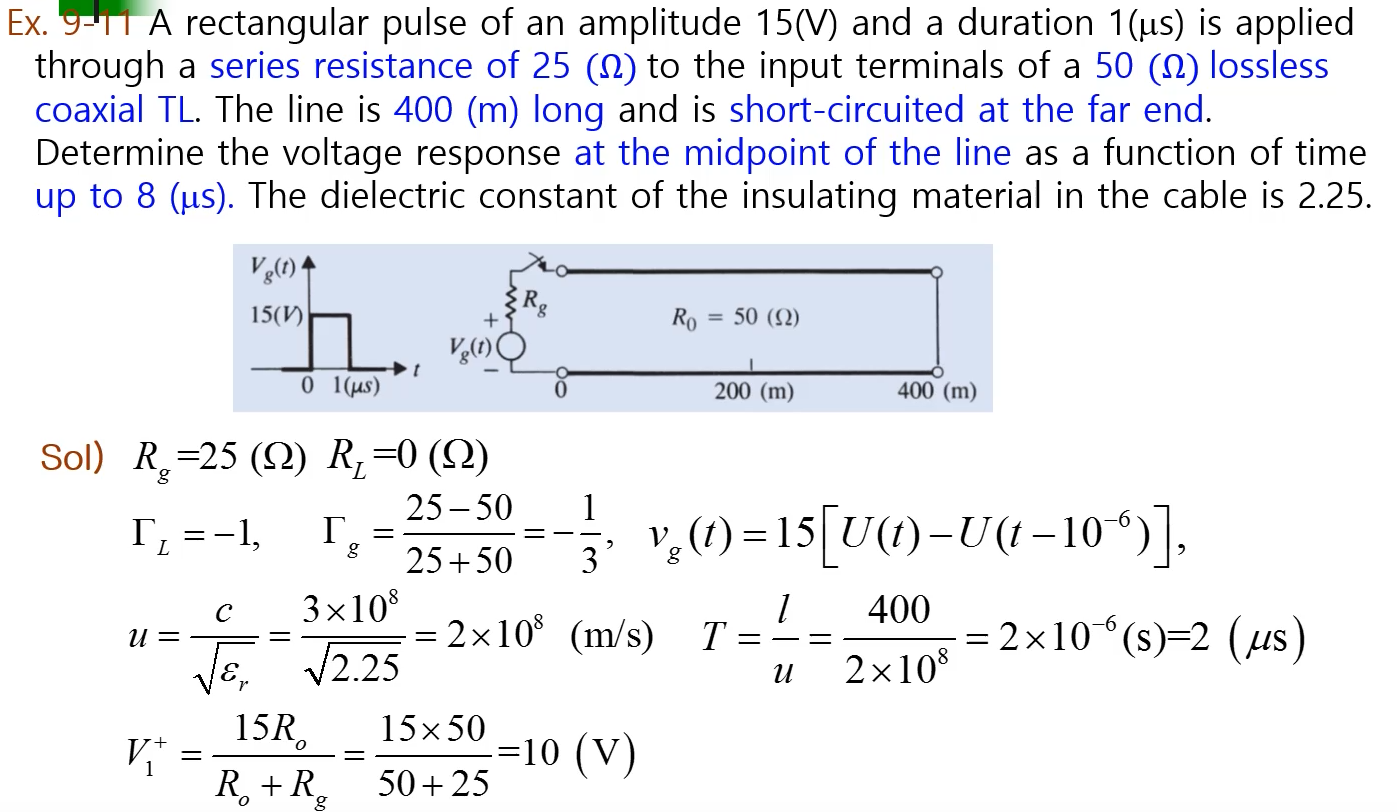
부하가 쇼트되었을 때
Rg는 25옴 속도를 구해서 T를 구해주면 되겠다
펄스 폭이 1마이크로 세컨드 T는 2마이크로 세컨드
이경우에 나타나는 현상을 보도록하자.
각각의 위치의 전압을

오른쪽 그림은 위의 두개 그림을 아래로 합친것
대전된 선로에 부하를 연결하게 되면 부하 양단에 숏펄스가 만들어지는 원리를 보도록하겠습니다.

R양단에 Vr이 발생하는데 그럼 숏펄스가 만들어지게 된다
회로를 바꾸면 전송선로가 있고 V0로 충전이 되어있고
부호가 반대로 연결되있다고 생각해보면 전체전압은 0
두가지 회로의 중첩으로 보면 왼쪽의 회로를 보면 V0가 있고
V0로 충전되어있어서 같은 전압이 마주보고 있어서 이 경우에
스위치를 닫아도 변화가 없다.==>병렬로 연결되어있어서
선로상의 전압을 C번 그림에 중첩하게 되면 V0 전압을 구할 수 있다
R 양단의 전압을 구할 수 있다.
선로의 전압은 V0였다가 V0/2가 되어서 줄어들어서 이동을 하게 됩니다.
이상태에서 반사를 생각하면 끝에서 오픈 밴드여서 반사계수가 +1이죠
-V0/2 인풋 단자에서 생각하면
선로 양단의 전압은 V0/2가 발생했다가 다시 0으로 가게 된다.
t=2l/c가 됬을 때 R양단의 전압은 스위치를 닫으면 0에서부터

펄스가 발생한다.

전류에 대해서도 생각해보면 짧은 펄스를 만들 수 있다.
충전했다가 스위치를 닫게 되면 숏펄스를 만들수가 있다==>레이더에서 매우 짧은 펄스를 만들어서
그런 회로로 응용이 되곤합니다.

부하가 인덕터나 캐패시던스로 되어있을 때 나타나는 현상을 알아보자

입사파와 반사파가 트랜지언트 형태로 나타나는 경우
V1+가 가해지면 V0/2 오른쪽으로 이동하게 된다
반사가 일어나게 되는데 t>T일 때 V1+와 V1-가 나타나는데
VL에 관해서 식을 써보면 이것을 V1-를 대입을 하면 Vl은 2V1+-R0iL
Vl대신에 인덕터 식을 대입하면 전류에 관한 미분 방정식을 구할 수 있다.

t인 순간에 전압이 가해졌을 때 전류가 흐르지 않고
iL(무한대)는 2V1+/R0 ==> 쇼트에 가까워서 2배의 전류가 흐르게 됩니다.
첫번째 바운더리 컨디션을 적용

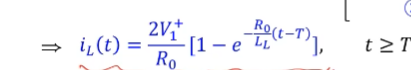
전압은 미분을해서 구할 수 있다.
V1-는 Vl과 V1+로부터 구할수 있다.


캐패시턴스가 연결되있을 때도 동일하게 구할 수 있다.

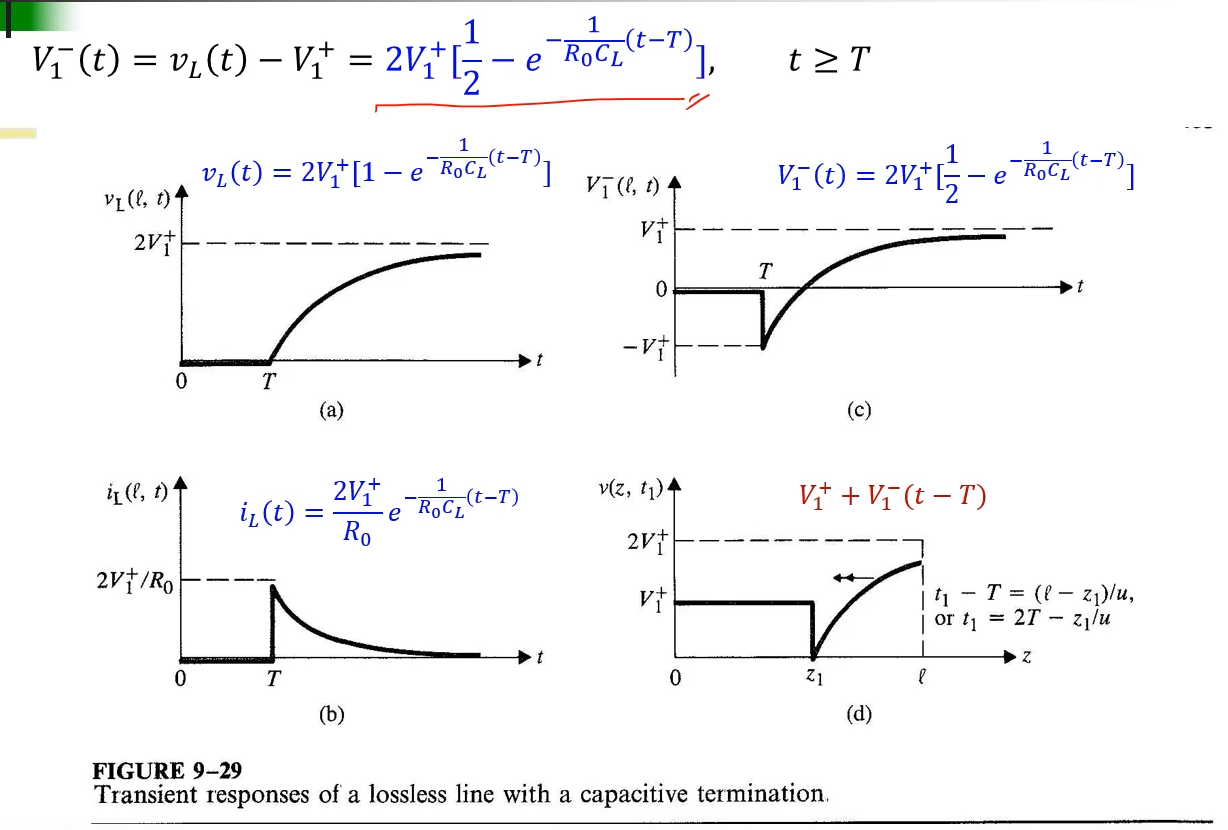

고주파 회로를 해석하는데 매우 중요한 내용이 된다
타임하모닉 스태디 스테이트에서 나타나는 여러가지 전송선로에 대해서 계산했는데
차트를 이용해서 구할 수 있고 개념을 이해하는데도 매우 편리한 차트가 될것 이다.

감마 플레인이다. 노말라이즈 임피던스를 그려놓은것입니다.
감마 플레인에서 감마라고 하는것은 일반적으로 R값이 양값일 경우
플레인 상에서 저항과 리액턴스 값을 R과 x를 알수 있다.
차트를 구하기 위해서 감마를 생각해야 되는데

감마도 컴플렉스로 나타나게 된다.
리얼파트와 이메지너리 파트로 나눈다.
특성임피던스로 부하임피던스 나눠준것을
normalized 임피던스 zL R과 x를 알면 대문자 ZL을 구할 수 있다
정규화된 임피던스를 이용해서 풀고 실제 임피던스로 변환 가능하다.
Rx와 감마 사이에 어떤 관계가 있는지 알아보자.

분모를 유리화해서 분자의 식을 구하면 위와 같은 식으로 나오게 된다.
r값의 변화에 따라서
x값의 변화에 따라서 어떻게 변하게 되는지
매우 알게 쉽게 유도한 사람이 스미스이다.
R의 크기에 따라서 원의 방정식으로 표현할 수 있다.
첫번째와 두번째 식을 각각 원의 방정식으로 변환했다.
첫번째 방정식

r값에 따라서 센터와 radius가 주어지는 원의 방정식으로 나타나게 된다
감마r과 감마i의 플레인에서.
r값이 커질 수록 원점으로 다가가게 된다
두번째 equation



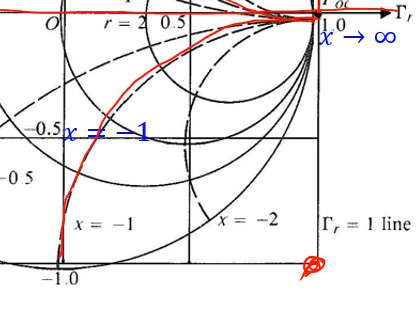


인덕티브 로드면 위쪽에 점이 찍히게 되고
캐파시티브 로드면 아래쪽에 그림에 찍힌다.
왼쪽은 쇼트 오른쪽은 오픈 감마i값에 따라서 인덕티브와 캐패시티브가 바뀐다.


감마와 zl과 직접적인 연관 관계가 있다.
Zl로부터 이동을 한다. z'지점으로부터 이동을한다.
차트를 이용해서 구할 수 있다
감마의 관계를 보면 부하에서의 관계
임의의 위치에서 로드에서 감마에 e^-j2Bz'
한바퀴회전하면 길이 얼마에 해당하겠느냐
반파장마다 회전하게 된다
0.25람마 마다 반바퀴 회전
wavelength toward generator
wavelength toward load
두가지 방향이 다르다.
부하쪽으로 이동하느냐
전원쪽으로 이동하느냐

Rl=R0일 때 센터가 된다
원의 반경이 작아지면 r값이 점점 작아진다.
제일 바깥쪽이 r이 0일때
0.1부터 0.9까지 표시가 되어있다.
아래쪽은 -로 읽어야 한다.

r0를 곱해주면 실제 부하의 임피던스가 된다.

감마의 크기는 자로재서 그대로 읽는것이 아니라
반지름이 1이라서 B/A 한것이라서 길이만 재는것이 아니라 나눠줘야한다.
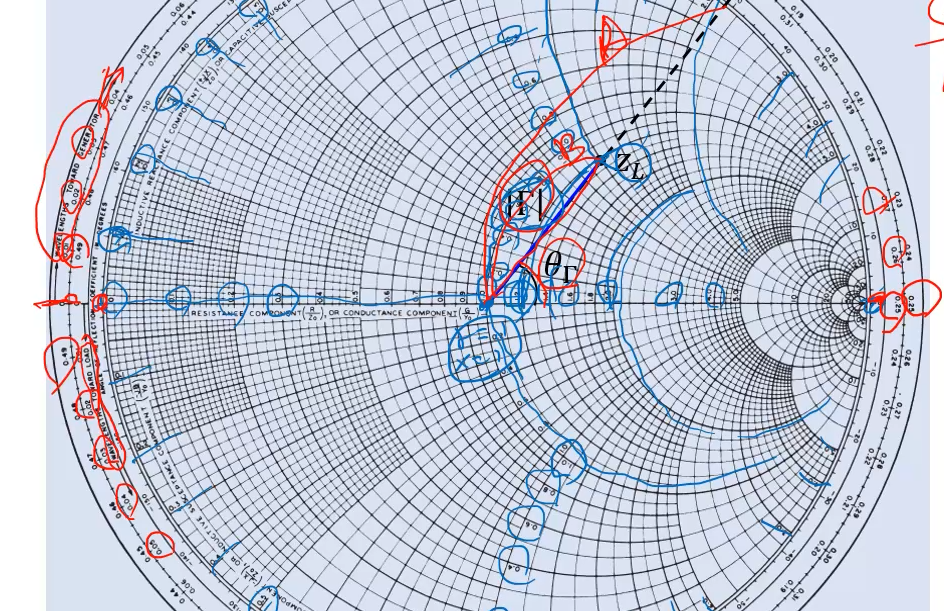
wavelength toward generator
wavelength toward load
방향에 따라서 숫자가 써져 있다.

Zl로부터 0.1 람다 이동했을 때 값이 얼마냐?
회전을 시키면 된다. 0.277 정도가 된다.
웨이브 랭스만큼 회전 시키면 된다.
부하로부터 전원쪽으로 이동했을때 인풋임피던스의 변화를
회전시켜서 읽어줄수 있게 된다!
부하쪽으로 이동하느냐 제너레이터로 이동하느냐에 따라서
어떻게 회전시켜야할지 판단해야한다

감마의 크기가 고정되있는 서클 상에서
S 파라미터는 같게 된다.
선로에서 ZL에 선로에 이동을 하게 되면 ZL로부터 회전하게 되는데
회전하면 스탠딩 웨이브가 나타난다
감마에의해서 전압과 전류의 변화가 나타나게 된다.
ZL로부터 이동하더라도 감마의 크기가 일정하고 S 파라미터는 일정하다
부하로부터 이동할 때 전압의 맥시멈과 미니멈이 나타나는데

ZL로부터 이동하다가 PM 지점을 만나면 x=0, r>1이어서 전압의 맥시멈 위치가 된다.
부하로부터 이동했을 때 전압의 맥시멈이 나타난다.

램다/4만큼 이동하면 전압의 미니멈이 나타나고 전류의 맥시멈이 나타난다.
전압의 맥시멈이 나타나는 위치에서 r>1일 떄
S값은 Rl/R0가 되는데 ==r이다.
즉, Pm 지점에서 S=r이 된다.
Pm지점의 r값을 읽으면 S가 된다.
특정지점의 부하가 ZL이다.
ZL에 대한 스탠딩 웨이브 레이시오는
PM지점의 r값을 읽으면 S가 된다.

pm 지점에서는 1/r이되어서 같지가 않다.
반드시 PM지점에서 r값을 읽으면 스탠딩 웨이브 레이시오가 된다.
퀴즈
감마플레인에서 r과 x에 따른 그래프를 그리고
스탠딩 웨이브 레이시오를 읽는 방법을 얘기하고
볼티지 맥시멈과 미니멈이 나타나는 위치를 얘기하기 바랍니다.
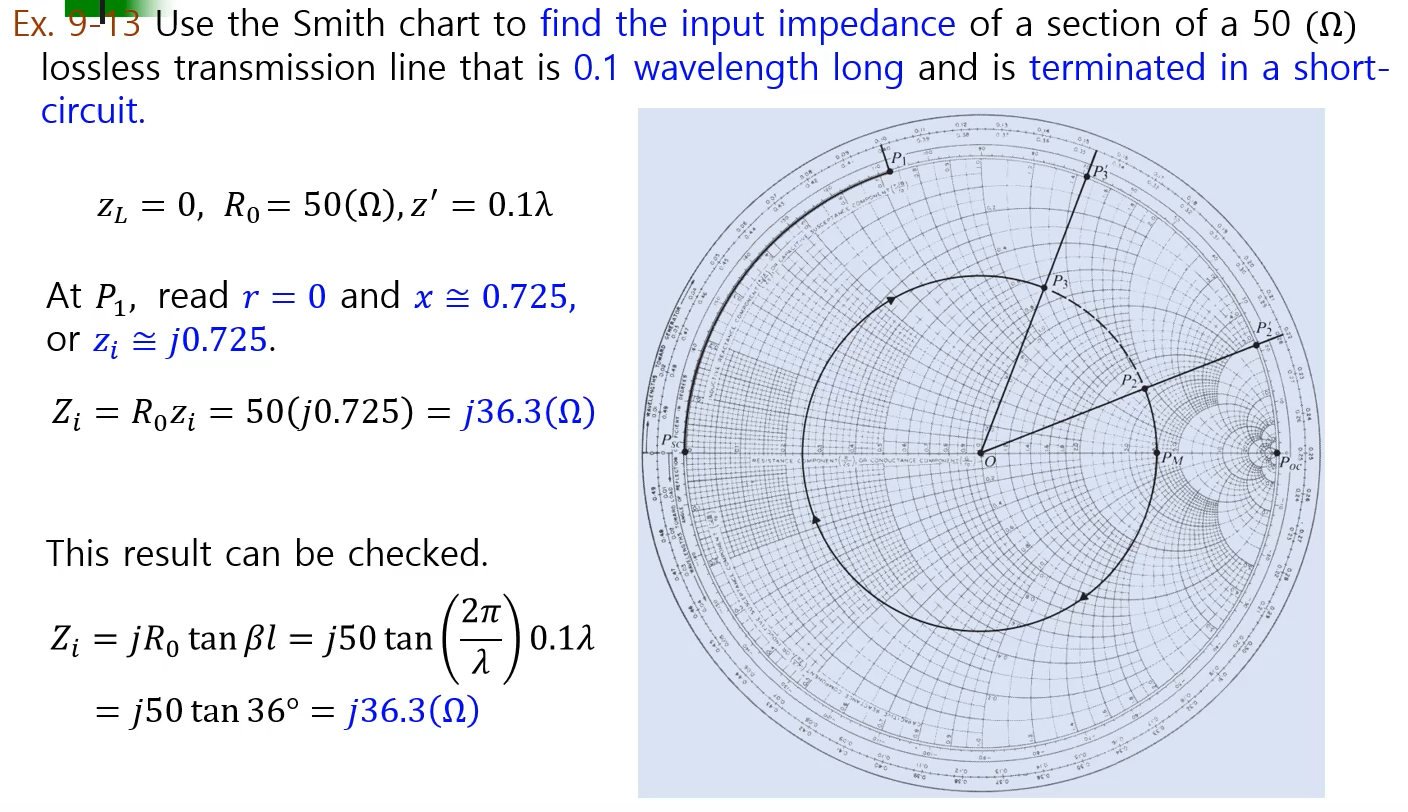
쇼트로부터 0.1 웨이브 랭스만큼 이동했을때 들여다본 인풋임피던스가 얼마일까
쇼트된지점으로부터 0.1 웨이브 랭스만큼 회전시키면 P1지점이 된다.
여기서의 r과 x 값을 읽으면 r은 0이고 x는 0.725정도 된다.
Zi=R0zi 즉 50옴을 곱해줘서 구할 수 있다.

볼티지 리프렉션 상수 감마가 얼마인가
Zl위치에 관해서 찍어야 한다.

2.6+j1.8 P2 지점이 2.6+j1.8


0.434 람다일때 인풋 임피던스는 얼마인가


'RF 시스템 설계 > 전자기학II' 카테고리의 다른 글
| 전자기학II [평면파~전송선로 이론][8장~9장 정리] [完] (0) | 2020.12.16 |
|---|---|
| The Smith Chart & Impedance Matching [完] (0) | 2020.11.30 |
| Finite Transmission Lines (0) | 2020.11.22 |
| Transmission Lines (1) | 2020.11.14 |
| Oblique Incidence at a Dielectric Boundary (0) | 2020.11.06 |