


평행편판에 TEM 웨이브가 전송될 때
전송선의 선로에서 전류와 전압을 유도한다.
제너럴 전송선 방정식이라고 해서 전송선에 손실이 있을 때
전송선로 방정식을 유도하고 선로에 관한 파라미터를 구하겠습니다.

두 도체에는 전하가 유기되고 전류도 유기됨으로써 전압 전류가 발생해서
전압이나 전류가 어떤 형태로 전송되는지 이야기 해보자.


전기장은 y방향
자기장은 -x 방향으로 발생할 때
z방향으로 전송이 된다고 가정한다.
단면방향으로는 균일하다, 크기 위상 균일하다고 가정한다.
컨덕터는 퍼펙트 컨덕터 두 도체사이 다일렉트릭이 있는데
시그마는 제로라고 가정
TEM 웨이브가 전송되고 있는데

평면파에관한 식으로부터 페이저 형태로 쓸 수 있다.

플레이트에 발생하는 표면전류가 어떻게 될까
두 도체 사이에서 TEM 웨이브가 전송
위쪽 플레이트와 아래쪽 플레이트 사이에 발생하는 표면전하를 보자
아래쪽 플레이트에 발생하는 표면전하를 보면
an벡터는 ay벡터가 될것이다. =>+ 전하가 발생한다.
an x H가 surface 커런트 az방향이 되서 아래 도체에 발생한다.
위쪽에서는 -ay벡터
표면전류는 -차지가 된다.
전류는 -az 방향으로 발생한다.
표면 전류는 -입실론 E0 타임도메인으로 바꿔보면


전하가 발생해서 전체 모양이 타임이 증가하면 오른쪽으로 이동한다.
위쪽에는 - 아래쪽은 +
양단에 전압이 발생하는데
전압도 웨이브로 프로파게이션 한다
어퍼플레이트의 전류를 보면 -az방향으로 =>선로의 진행방향
에타분의 E0 전류를 보면 코사인 함수로
전류가 처음에는 -z방향으로
+z방향으로 전류가 발생한다.
로우 플레이트는 부호가 +가 되서 플러스 방향으로 전류가 발생
전체 모양이 오른쪽으로 이동한다.
전류는 H필드에 의해서 발생한다.
H필드가 x방향으로 발생하니까 z방향으로 전류가 발생한다.
자기장도 전기장과 같은 위상으로 발생하니까
z방향으로 전류가 유기되서 전류 웨이브가 발생해서
마찬가지로 오른쪽으로 속도 up로 발생한다.
TEM 웨이브에 상응하는 전류와 전압이 발생해서
같은 속도로 TEM 웨이브로 이동한다.
전압이나 전류를 사용해서 표현하도록한다.
TEM 웨이브가 전송될 때 맥스웰 방정식으로 전압과 전류를 유도해서
어떠한 형태로 나타나는지 살펴보자.

전압과 전류에 관한 표현식을 구해보도록 하겠습니다.
맥스웰 방정식을 써놓고
전기장은 Ey 자기장 식은 Hx
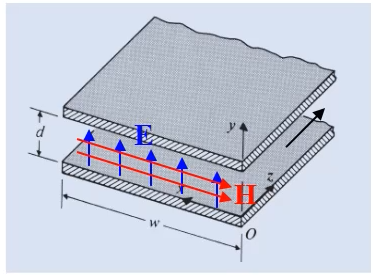
맥스웰 방정식에서 x방향 y방향으로 변화가 없고
z방향으로 변화하니까
컬을 취하면 z방향으로만 남게 된다.
z만의 함수여서 상미분 방정식이 된다.
Hx에 관해서 미분하게 되면 컬을 취해보면 y방향 성분이 되고
오른쪽 항은 둘다 y방향이 되서
막스웰 방정식은 TEM 웨이브가 전송되고 있으니까
커플드된 미분 방정식으로 쓸 수 있다.
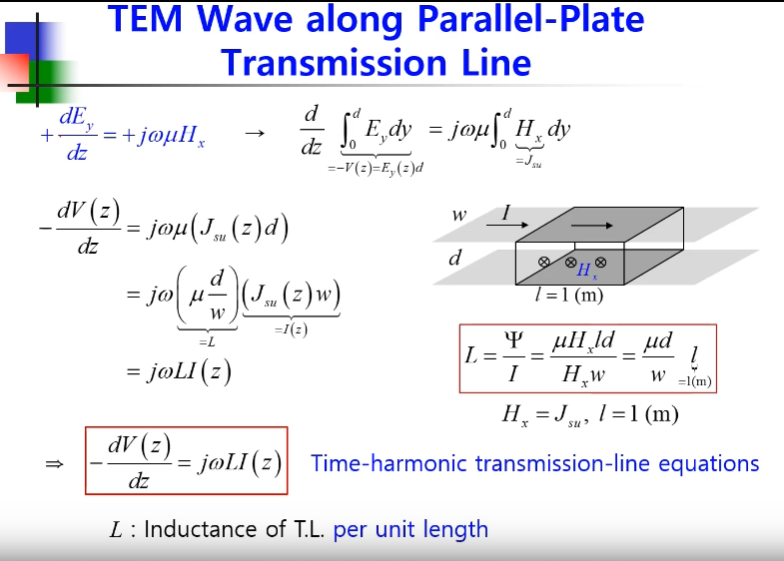
둘다 마이너스가 있는데 +으로 바꾸고
양변에 대해서 y방향으로 적분하도록 하면 -V가 되고
오른쪽의 Hx는 Jsu d 가되고 왼쪽것은 -V(z)
Jsu곱하기 d가 아니라 Js곱하기 w로 곱해주면
w로 나눠주고 d로 곱해주고
평형평판에서 단위길이당 인덕턴스
단위 길이당 인덕턴스가 된다는것은
인덕턴스를 구하는 기본적인 원리로부터 구할 수 있다.
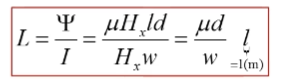
인덕턴스는 사이를 통과하는 총 자속을 나눠준것
전류I는 Jsu에 w를 곱해주면 Hx와 같고 Hx는 캔슬되서 없어지고
단위길이당 인덕턴스가 된다.
-dV(z)/dz= jwLI(z) 전압과 전류에 관한 식으로 변화한다.
z에 관한 미분식으로 쓸 수 있다.
전송선 방정식이라고 부른다.

두번째 방정식을 구해보자

w방향으로 적분해보도록 합시다.
Hx라고 하는것은 Jsu*w해서 I(z)
E(y)*d가 -V가 되니까

TEM 웨이브에 관한 맥스웰 방정식 두개의 식으로부터
전압과 전류에 관한 일차미분 방정식을 얻을 수 있다.

연립미분방정식을 구하기 전에
방정식 의미를 보면 델타 z라는 선로가 있는데
선로의 길이를 델타z라고 본다.

선로에 관한 전압 전류가 표시가 되는데
전압 전류의 관계가 회로적으로 어떻게 표현할 수 있는지 보도록 하자.
델타 z가 미분식을 다시 쓰게 되면 델타 z를 오른쪽으로 넘기게 되면
쓸수가 있다. 두번째 식도 전류에 관한 식으로 쓰게 되면
jw(c델z)v(z)
미소 길이의 전송선로를 등가회로로 변환 가능
키르히호프의 전압 법칙 V(z)에 V(z+델타z)
두 전압 사이에 L델타z라는 인덕터가 연결되어 있을 경우
두 지점의 전위차가 L델타z의 인덕터가 있는것 처럼 나타난다.
전류는 두 지점사이의 전위차 V(델z+z)
사이의 캐패시터가 있는것으로 볼 수 있다.
미소 길이에 대해서 직렬로 L 병렬로 C
이러한 회로가 계속해서 연결되어 있는 회로로 모델링 할 수 있다.

회로가 쭉 연결되어있을 경우 흘러들어가 전류가 있고
양단의 전압이 있으니 각각의 위치가 딜레이되서
오른쪽으로 전송된다.

전압에 관한 이차 미방, 전류에 관한 미분 방정식
전압이나 전류가 크기만 다를 뿐 같은 형태로 propagation 된다는 것을 알 수 있다.
전파상수가 같아서 속도도 같고 파장도 같다.
+z 방향으로 전송선로가 있으면
-z 방향으로 진행하는
임피던스 매칭이 되어있지 않으면 반사파가 존재하고
매칭되거나 선로가 무한히 길면 반사파가 존재하지 않는다.
반사파가 없는 경우를 알아보자

전압과 전류의 비를 Z0라고 두자 => 전송선로의 특성 임피던스
플레인웨이브가 전송될때 전기장 자기장 비를 고유 임피던스라고 했는데
전송선로에서는 반사가 없을 경우 전압과 전류의 비를 특성 임피던스라고 부른다.
선로에 임피던스가 잘 설계되어야 전송선로로 구성된 회로를 이용할 수 있다.
방정식에서 dV(z)/dz
전압과 전류의 비를 구해보도록 하자.
V에 관해서 미분하게 되면 -j가 빠져나오고
평행편판에 특성임피던스를 구해보면
에타에 w분에 d
특성 임피던스를 보면 두 선로 사이의 간격
선로의 형태에 따라서 선로의 임피던스가 달라진다.
위상 속도
뮤입실론 분의 1과 같은 값이 된다.

LC분의 1로 TEM웨이브가 전송되는 속도로
전압 전류 웨이브가 전송되게 된다.
전송선로 방정식, 특성 임피던스 ,속도, 전압,전류 웨이브의 형태
도체는 시그마가 무한대 두 도체 사이에 다일렉트릭이 있는데
그 사이의 시그마가 0일 때 가정하고 해를 구했죠
시그마가 존재할 때 저항 또는 컨덕턴스가 있어서 손실이 발생한다.
어떤 손실이 있는지 알아보도록 하자.

평행편판에 손실이 없다고 생각하고 방정식을 유도했는데
실제로는 손실이 존재하니까 손실의 요소에 대해서 생각해보자
두개의 판이 평행편판 사이에 입실론이 있는데
시그마가 있는 경우 두 판사이에 전류가 흘러서 손실이 발생
도체 자체가 완전도체로 가정했는데 시그마가 무한대가 아니고
파인하다. 첫번째 케이스=> 컨덕턴스 G에 의해서 손실이 발생하고
R 단위길이당 저항 성분에 의해서 손실이 발생한다.
두가지 성분에 의해서 손실이 발생한다.

G라고 하는것은 두 컨덕터 사이에 시그마가 존재하는 경우에
두 판사이의 컨덕턴스를 구할 수 있는데
캐패시턴스를 알고 있으면 구할수가 있죠
그것을 이용해서 G를 구할 수 있다.
단위 길이당 컨덕턴스.
윗면과 아랫면에 의해 발생하는 직렬저항을 계산해보면
판의 두께가 존재한다고 할 때
고주파이기 때문에 도체의 표피 두께
skin depth 델타에만 전류가 흐르는것으로 볼 수 있는데
단면에 대해서만 전류가 흐른다.
시그마를 해주게 되면 직렬 저항값이 된다.
저항값은 시그마에 컨덕터에 시그마가 되고
저항값을 구할 수 있다.

판이 위의 판이 있고 아래 판이 있으니 두배를 해서 저항값을 구할 수 있다.

우리 책에서는 판이 존재하면 전기장은 y
자기장은 x방향 전류 Jsu가 z방향으로 흐르는데
시그마c가 무한대면 Jsu가 흘러도 z방향의 전기장은 발생x
하지만 시그마가 무한대가 아니게 되면 전류가 흐른다는 얘기는
일렉트릭 필드가 발생한다는 말이다.
z방향의 작은 전기장이 발생한다=> 퍼터베이션이 발생한다.
도체안에 Ez가 약간 발생한다는것이다.
도체 내부에서 전류가 흐르면서 전기장이 발생한다.

도체가 존재하는데 내부에서 소모되는 전력은
포인팅벡터를 할 때 얘기한것 처럼
ExH가 포인팅 벡터가 되는데 이 표면을 적분하면 전력이되서
내부에서 소비되는 전력이랑 같다.
도체 표면에서 y방향의 포인팅 벡터를 구하면 소모 전력과 같다.
도체 내부에서 전류가 흐르면서 이러한 성분이 존재한다.
계산하기 위해서 surface 임피던스를 계산하게 되는데
표면 임피던스는 Et/Js를 임피던스로 정의하고
어퍼 플레이트에
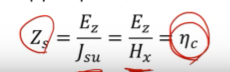
Ez/Hx 도체 내부의 고유 임피던스가 된다.

로시 미디움에서 얘기할때 고유 임피던스를 얘기한적이 있다.
도체 내부의 임피던스가 표면 임피던스랑 같다!
단위 면적당 전류 밀도 p시그마
토탈 파워는 p시그마에 폭을 곱해주게 된다.
(1/2)*I^2(Rs/w)
Rs에다가 w를 나눠준값이 R이 되는데
거기에 두배를 해줘야한다.
그렇게 하면 Rs를 이용해서 쓸 수 있다.
Rs/w 저항값을 구할 수 있다.
표피 두께를 가지고 구한값을 구할 수 있다.
Rs를 가지고 저항값을 구할 수 있다.

전송 선로에서 특성을 구하는데 중요한 역할을 한다.

기판에 대해서 그라운드가 있고
폭을 w 높이를 d 라고 뒀을 때

평행편판에 경우 위와 같은 전기장이 형성된다.
두개 판이 wm 판이 마주보고 있는것으로 생각하고 계산할 수 있다.
유효 유전율 내에서 마주보고 있는 판으로 해서 계산하면 된다.
그라운드 판이 아래 위로 있는 경우가 되겠다.
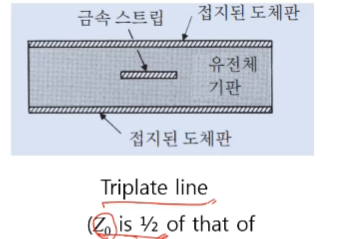
Triplate line에서는 C가 늘어나서 특성 임피던스가 반으로 줄게 된다.

2mm 폭을 만들면 50옴이 된다.

선로의 폭이 선로의 특성을 결정짓는데 중요한 역할을 합니다.

손실을 포함한 전송선로 방정식

일반적인 전기회로에서는 파장이 매우 길기 때문에
소자라고 하면 discrete한것으로 볼 수 있는데
각각 집중 소자로 얘기할 수 있다.
그래서 회로와 회로 사이를 연결하면 공간적으로 차이가 없는것
선과 선 사이에 전류의 변화가 일어나지 않는것
파장이 매우 짧아졌기 때문에 회로 자체가 파장의 몇배가 되기도 해서
위치에 따라서 달라진다.
선로가 연결되있을 경우 분포정수 회로로? 분석을 해야한다.
저항성분과 컨덕턴스 성분이 포함되어 있을 때

컨덕터에 저항이 있을 경우에 유전체에 손실이 있는 경우
전압과 전류에 관한 방정식을 세울 수 있다.
L C 이렇게 미소길이 대해서 전송선로의 경우 할 수 있는데
위상이 계속해서 지연되기 때문에
등가 회로로 변형을 시킬 수 있다.

회로의 등가회로가 표현이 된다면 위치에 따라서 파동이 위상이 점점 빨라진다.
우리가 생각하는 선로하고는 특성이 달라진다.
우선 전압법칙을 적용해서

전압과 전류에 관한 식을 얻는다.

전류 법칙을 적용하면
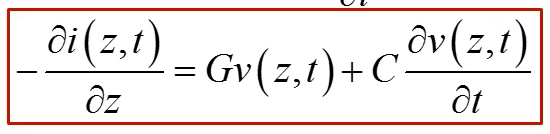
i와 v에 관한 식을 세울 수 있다.
시간에 관한 함수로 되어 있다.
장이 시간따라 정현파의 형태로 변화한다고 가정한다.
페이저에 t에 관한 미분은 j오메가로 바꿀 수 있으니까 R+jwL
t에 관한 미분이 없어져서 j에 관한것으로 나타낼 수 있다.
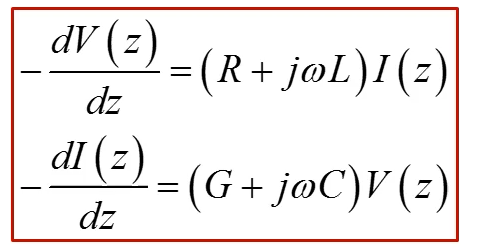

전압과 전류에 관한 솔루션을 구할 수 있는데
한번더 미분해주게 되면 커플드 time-harmonic transmission line equation을 구할 수 있다.

V와 I로 해를 쓸 수 있다.

전압과 전류 사이의 비를 특성임피던스로 했는데


진행방향이 바뀌면 부호도 바뀐다.

위와 같이 표현가능하다.
반사파에 대한 전압과 전류에 관한 -V/Z0가 된다. 매우 중요한 이야기

파동으로 이해해도 되는데 위와 같이
+z 방향으로 진행할 때 전기장과 자기장이 z방향으로 이동
전기장은 전압에 해당되고 자기장은 전류에 해당된다.
-z 방향으로 진행하는 웨이브는
전기장이 -z 방향으로 진행하면 Hy가 -방향으로 발생
전류는 부호가 -Hy로 해서 반대로 가게 된다.
출석퀴즈
제너럴 트랜스미션 라인 로스 있는 경우
타임 하모닉일 경우
솔루션을 구하고 전파상수 감마도 구하고
특성임피던스를 구해보도록 하고
입사파와 반사파에 관한
+방향으로 진행하는 웨이브
-방향으로 진행하는 전압 전류 웨이브의
관계에 대해서 쓰도록 해보자.

솔루션들은 로스 미디움에서의 솔루션과 비슷하게 나온다.


감마와 Z에 관한 식도 거의 유사하다.

세가지 중요한 케이스
로스리스 라인 R=0,G=0
감쇄 없고 주파수에 관해서 선형
특성임피던스가 리얼로 나타난다.

로우 리스 미디움에서와 비슷하게
디스퍼션, 디스토션이 일어나지 않는다.
특성임피던스를 보면 저항 성분은 로스 리스와 같고
허수 파트는 매우 작아서 0으로 근사가능하다.

디스퍼션이 일어나지 않는다.
리얼파트가 상수, 허수 파트가
위상속도가 컨스턴트
특성임피던스를 구해보면 R만 나타나게 된다.
손실이 존재함에도 불구하고 허수파트가0
디스토션 디스토션이 일어나기 위해서는
속도가 주파수에 따라 달라지면 디스토션,퍼션이 일어나고
위에있는 디스토션리스 라인이 아닌경우에 로우 로스라든지 로스가 매우 적은
이런 경우에 우선 주파수에 따라서 속도가 달라지지 않는다.

디스 토션 리스라인에 조건을 만족하면 알파도 상수, 속도도 상수
로시미디움에서는 논리니얼이기 때문에 디스토션이 일어난다.

R0=50옴


다른 형태의 전송선로에 대해서 파라미터가 어떻게 되는지 알아보자

선로가 있을 때 입실론과 시그마가 있는데
TEM 웨이브 전송속도와 전압전류 이동속도랑 같다
C를알고 있다=>L을 구할수 있다.
셋중 하나 알면 나머지 알 수 있다.

저항값을 구할 수 있다.

파워 관계를 이용해서 알파를 구해보자



'RF 시스템 설계 > 전자기학II' 카테고리의 다른 글
| Transients on Transmission Lines (0) | 2020.11.29 |
|---|---|
| Finite Transmission Lines (0) | 2020.11.22 |
| Oblique Incidence at a Dielectric Boundary (0) | 2020.11.06 |
| Conducting & Dielectric Boundaries (0) | 2020.11.05 |
| Electromagnetic Power Flow & Conducting Boundary (0) | 2020.10.23 |