


반사파가 없는 경우에 대해서 얘기했었는데
이번에는 유한한 경우 부하가 있을 경우랑 없을 경우
앞으로 이동할 수록 임피던스가 달라지게 된다
전송선로를 이용해서 임피던스 매칭이 일어나는데
부하가 연결될 때 반사계수를 알아보고
임의의 저항이나 임피던스가 연결될경우 나타나는 현상
전송선로 circuit을 알아보도록 합시다.
이번주 내용은 전송선로 반사계수 임피던스 변화 등등 중요하겠습니다.


부하가 매칭 되어있지 않을 때
전류는 +- 디파인하고
전압은 -+ 디파인한다.
+방향으로 진행하는 전류 전압 웨이브
-방향으로 진행하는 전류 전압 웨이브
동시에 존재한다.
전류는 특성임피던스로부터 구할 수 있다.
V0+나 V0-를 구하면 선로상에 나타나는
전류 전압을 모두 구할 수 있다.

선로가 매칭되어있으면
로드 임피던스가 특성임피던스랑 같을 경우
반사파가 0이된다.

임의의 부하가 연결되어있을 때
선로 상으로 진행하는 V+와 I+
V-,I-가 존재하는데
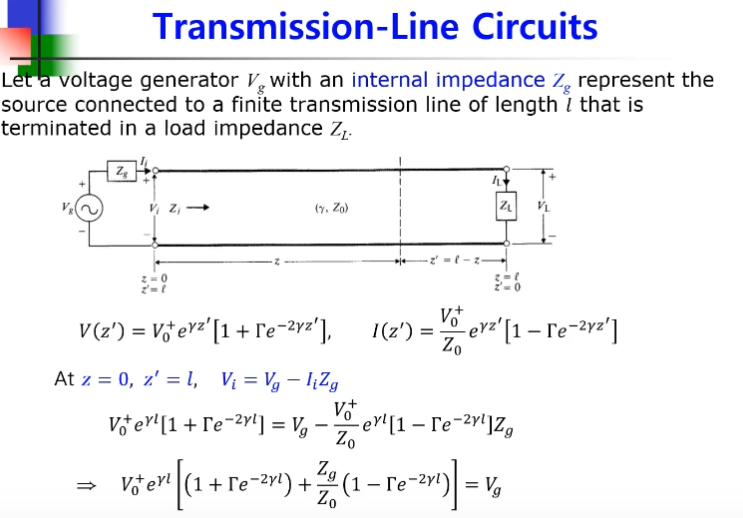
전체 길이가 l인 전송선로를 연결하고
부하Zl을 연결했다고 봅시다.
우선, 인풋단자를 z=0일 때
부하 위치에서 부하 양단의 전압이 Zl이 되고
선로 상에는 +와 -로 진행하는 웨이브가 동시에 있어서
임피던스는 두
+방향으로 진행하는 웨이브와
-방향으로 진행하는 웨이브가 동시에 존재해서

특정 위치에서 임피던스는 합친 전압 또는 전류의 비를 임피던스다.
감마,베타,속도up 등등 이런 값들이 추가가 되어야 선로의 특성을 나타낼 수 있다.
길이 L인 선로에 인풋단자 Vi Ii 인풋단자에서 들여다본 인풋임피던스를 계산할 수 있다
V+와 I+에 의해서 Zl이 있고 V-와 I-가 발생하게 되는데
반사파가 얼마나 발생하는지 구해보도록 하자.
선로 상에는 +방향으로 진행하는 웨이브와
-방향으로 진행하는 웨이브가 있는데
웨이브 사이의 관계를 이용해서
V0+와 V0-의 크기를 계산해봅시다.

전압과 전류에 대해서 식을 세우고
V0+와 V0-를 먼저 구해보도록 합시다.
Vl=IlZl


l-z가 의미 하는것

z'은 현재 위치에서 부하로부터의 거리를 의미한다.
전송선로를 따라서 얼마나 이동했느냐?

하이퍼볼릭 함수를 이용해서 표현 가능하다.

선로상에 임의의 위치에서 V(z)' I(z)'을 구했다.
선로 상에 임피던스는 Zl=Vl/IL
이동하다보면 인풋 임피던스는
부하 쪽을 바라본 임피던스가 되는데

전원쪽으로 바라보면 다른값이 나온다.

웨이브 임피던스 얘기할 때 얘기를 했었죠

만약 인풋 단자에서 보면 z' 대신에 l을 사용하면 됩니다.

등가회로로 바꿔서 Vi와 Ii를 구할 수 있다.
인풋 단자에 가해지는 전력을 구할 수 있다.
선로가 만약에 로스리스다.
인풋단자의 전력은 부하에서의 전력과 같다.

부하 임피던스가 매칭되었을 때
임의의 위치에서 Z0
반사파 없이 +방향으로 진행하고
크기는 Vi,Ii
부하가 매칭 되어있으면 무한히 긴 선로와 같은 모양으로 나타나게 된다.

선로의 속도로 주어져 있는데
아까는 감마,z0 주어줬었는데 선로 특성을 규정한다.
2.5*10^8
문제에서는 부하가 매칭되어있는데
만약에 매칭이 되어있지 않으면
전원의 저항까지 같이 고려해야 되서 문제가 복잡하게 된다.
이문제는 다시 나올것
첫번째로 임의의 위치에서 전류 전압을 구하라
그것을 구하기 위해서는 전류 전압
매칭이 되있으니 Vi,Ii가 V0+ I0+ 이렇게 될것이다.
식 값들을 정리하면 Vg=0.3 Zg=1~~ 이런 값들을 이용해서
Vi를 구하고 Ii를 구한다.

위와 같이 구하면 된다.
선로의 특성을 주면 나머지 값들을 구할 수 있다.

부하 쪽에서 전압 전류가 어떻게 되느냐?
인풋단자의 전력이 부하에 전달된다.

쇼트나 오픈되어있는 부하를 연결했을 때 선로의 길이를 적당히 조전함으로써 회로소자를 연결할 수 있다.
주파수가 300MHz가 넘어가게 되면

인덕터가 동작안하고 C로 바뀌게 될수도 있고~
여러가지 현상이 나타나게 된다.
전송선로를 이용해서 구현하는것이 유리하다.
선로가 로스리스일 때
인풋임피던스는


선로를 오픈시켰을 때
들여다본 Zi0라고 할 때
ZL이 무한대가 된다.
길이에 따라서 값이 달라지게 된다.
(Capacitive <=> Inductive)
오픈선로가 λ/4 보다 작으면 캐패시터가 된다.
λ/4가 되면 인풋 임피던스가 0가되서 쇼트가 되버린다.
선로의 위치에 따라서 인풋임피던스가
얼마나 크게 변하는지 알 수 있다.
λ/4를 넘으면 인덕터가 되고
λ/2를 넘으면 다시 오픈된다
λ/2마다 같은 현상이 반복하게 된다.

길이가 매우 짧을 경우에 캐패시터로 동작한다.

전송선로를 쇼트시켰을 때
처음에는 인덕턴스로 나타나다가 캐패시터로 동작한다.

길이가 매우 짧을 때는 인덕터로 작동

(2n-1)λ/4일 때
쇼트가 오픈이 되고 오픈이 쇼트가 된다(역수)

인풋단자에서 임피던스는 부하의 인벌스가 된다.
quarter-wave transformer는 임피던스 매칭하는데에도 사용되곤한다.
Zl을 부하로 해서 매칭을 시켜야 하는데
들여다본 임피던스가 Zi

λ/4 선로를 사용하게 되면
인풋임피던스와 Zl이 매칭되게 된다.


λ/2가 되었을 때 Zi=Zl이 된다.
원래 임피던스로 다시 돌아가게 된다.
이러한 경우에도 간혹 사용되는데
도파관 같은것을 연결시켜야할 경우
홈이 생기는데 웨이브가 진행하다가 홈의 영향을 받게 된다.
일부로 λ/2를 만들어서 커플링을 시킨다.
하프 웨이브섹션도 사용이 됩니다.

측정을 통해서 로스를 구하는 경우
선로의 특성을 모르겠다. 감마도 얼마인지 모르겠다
=>측정을 통해서 선로의 특성을 측정

network analyzer를 이용해서 넓은 주파수 범위에 대해서 인풋임피던스 zio와 zis를 측정할 수 있다.
쇼트를 시켜서 측정하고 오픈해서 측정해서 선로의 특성을 구할 수 있다.

오픈일 때는 - j54.6 오픈일 때는 j103
b번은 길이를 두배로 늘리면 어떻게 되겠는가?
쇼트시켰을 경우에 길이를 두배로 늘리게 되면 -j231
쇼트시켰을 때 1.5m일 경우 인덕턴스로 나타나게 되는데
길이를 두배로 늘리면 캐패시턴스가 된다.


저항성 부하가 연결되어있을 경우
반사계수를 어떻게 구하겠는가?

책보다는 조금 더 일반적인 방법으로 반사계수를 구하고 임피던스와의 관계를 알아본다.
Z0라는 전송선로 라인에 ZL이 연결되어있다.
+방향으로 진행하는 웨이브가 입사되었을 때 반대방향으로 진행하는 웨이브가 나타나고
감마를 정의하게 되면 V0+에 expnential
감마는 V0+/V0- 이렇게 정의한다.

부하 위치에서의 반사계수
전류는 V0+와 V0-를 사용해서 표현하게 되고
V0-대신에 감마로 표현을 할 수 있다.
반사계수를 구하기 위해서 부하 위치에서 경계조건을 사용하도록하자
VL/IL을 하면 ZL이 되는데
감마를 0으로 전류에

부하위치에서 감마를 구할 수 있다.
임의의 위치에서 컴플렉스 넘버로 나타나게 된다.

반사계수에 대한 식을 보면 다일렉트릭에서와 유사하게 나타남을 알 수 있다.

이식으로 부터 다시 Zl에 관한 식을 구할 수 있다.

ZL위치에서만 봤었는데 임의의 위치 z'에서 보게 되면
우리가 V0+와 V0- 를 대입하게 되면
임의의 위치에서 임피던스와 반사계수의 관계는 다음과 같다.
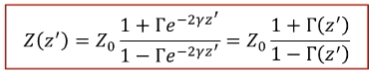


로스리스인 경우
손실이 없다고 가정했을 때


z'이 증가하면 회전하게 된다.
전압과 전류는 서로 미니멈과 맥시멈
λ/2 마다 한바퀴씩 회전하게 된다.
임의의 부하가 존재할 때 전압이 맥시멈이나 미니멈으로부터 출발하지 않고
λ/2 마다 한바퀴씩 회전한다.
출석 퀴즈
Z0인 선로에 부하 Zl이 연결되있을 때
반사계수를 구하고 임의의 위치 z'에서
무손실선로에서 전압과 전류의 표현식을 쓰고
벡터 그림을 이용해서 전압의 변화를 표시
임의의 위치에서 임피던스와 반사계수를 써라

감마에 따라서 ZL이 바뀐다.

부하가 저항성분일 경우 어떻게 변하는가
특성임피던스는 로스가 없는 R0
반사계수는 리얼넘버가 된다.
감마가 R0보다 크냐 작으냐에 따라서 +인지 -인지 결정된다.
RL이 R0보다 크면 0도(맥시멈)으로부터 변화

전류는 반대로
RL이 R0보다 작으면 미니멈으로부터 출발하게 된다.

오픈이나 쇼트가 되면 어떻게 되느냐
쇼트가 되면 RL=0
오픈일 경우 맥시멈에서 변하고
쇼트일 때는 미니멈으로부터 변한다.

스탠딩 레이시오로 부터 부하 임피던스를 알 수 있다.
Rl이 달려있고 R0가 있는 전송선로가 있을 때
R0가 얼마인지 모른다고 할때

변화하는것을 보면 크고 작음을 비교할 수 있다.
S도 측정할 수 있다.
S와 RL 사이의 관계를 알면 된다.

S:전압의 최대치/전압의 최소치

λ/4가 되었을 때


부하가 컴플렉스 일 때 부하위치에서 맥시멈이나 미니멈이 되지 않는다.
S를 측정하고
전압의 미니멈이 어디서 나타나는가?
그것으로부터 ZL이 얼마인지 구하라
전압이 변화하다가 멈췄는데
선로를 연장해서 저항을 달아서 Rm이라는 저항을 달아서
같은 형태의 스탠딩 웨이브가 나타나도록 Rm을 구한다.

Rm=R0/S
달아주면 같은 스탠딩 웨이브가 나오게 된다.
Zl대신에 길이 lm을 연장해서
들여다본 위치에서 ZL과 같다.
Rm을 lm 만큼 연장해서 달았을 경우
인풋 임피던스가 Zl과 같아지게 된다.
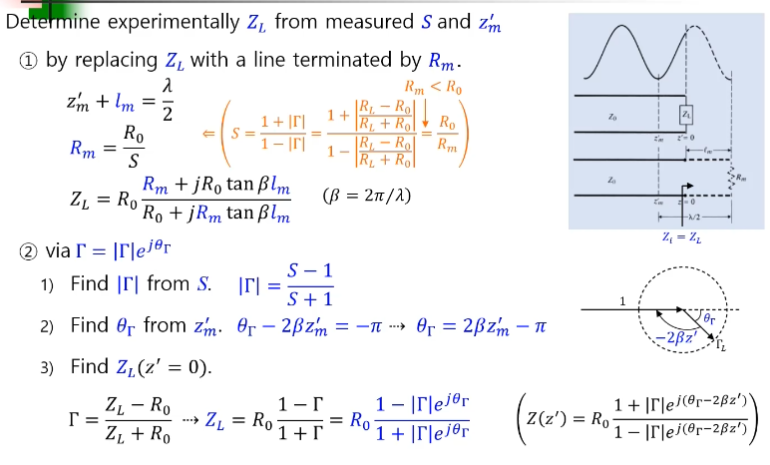
첫번째로 Zl을 구하는 방법은
lm은 λ/2에서 zm'을 빼주면 된다.
두번째 방법은
감마의 크기를 이용한다.

반사계수를 구해서 ZL을 구하라

lm과 Rm을 구하라



V1+V2+V3+~ 다 더했을 때 V(z')가 된다
==> 매칭되지 않았을 때 계속 반사가 일어난다.
무한히 반사==>수렴하게 된다.


임피던스 매칭이 되었을 경우


'RF 시스템 설계 > 전자기학II' 카테고리의 다른 글
| The Smith Chart & Impedance Matching [完] (0) | 2020.11.30 |
|---|---|
| Transients on Transmission Lines (0) | 2020.11.29 |
| Transmission Lines (1) | 2020.11.14 |
| Oblique Incidence at a Dielectric Boundary (0) | 2020.11.06 |
| Conducting & Dielectric Boundaries (0) | 2020.11.05 |