정전기장 정자기장 복습 [이택경 교수님 강의 6-4,6-3 정리]

전기장의 기본적인 두 가지 가정

전하로부터 발산하는 형태의 electric field가 발생한다. 

 

회전하는 전기장의 source는 없다.

 

양변에 체적적분을 해서 발산정리를 적용하면 가우스 법칙을 얻을 수 있다.

폐루프로 적분했을 때 값이 0이다. ==> 전기장은 보존장이다.

외부에서 가해준 힘을 적분하게 되면 0이 된다. 위치 에너지가 보존이 된다.

 

쿨롱법칙

포텐셜

포텐셜 차이는 1쿨롬의 전하를 P1에서 P2까지 이동할 때 외부에서 해줘야할 일의 양  

포텐셜을 구할 수 있다.

 

Electric displacement field

 

물질에 전기장을 가하게 되면 분극이 발생하게 되는데 분극이 전하와 같은 역할을 하게 되는데 전하에 의해서 발생하는 포텐셜로부터 등가적인 전하 로우 v를 구할 수 있다.

 

기존 전기장은 진공에 대해서 정의되었다. 그러나, 유전체 등의 편극성 물질에서는 

외부 전기장에 의해 분극이 일어나므로 이 물질의 효과까지 고려한 장을 생각할 필요가 있고, 

해당 장을 전기 변위장라 한다.

기호로는 D로 나타내며, 단위는 C/m^2이다.
여담으로, 이것의 자기장 버전이 자기장 세기이며, 기호로는 H로 나타내는 벡터 장이다.

 

유전율이란 무엇인가?

유전율(誘電率, 영어: permittivity) 또는 전매상수는 전하 사이에 전기장이 작용할 때, 그 전하 사이의 매질이 전기장에 미치는 영향을 나타내는 물리적 단위이다. 매질이 저장할 수 있는 전하량으로 볼 수도 있다. 같은 양의 물질이라도 유전율이 더 높으면 더 많은 전하를 저장할 수 있기 때문에, (저장된 전하량이 동일할 때)유전율이 높을수록 전기장의 세기가 감소된다. 그래서 높은 유전율을 가진 물질을 축전기에 넣는 유전체로 사용하면, 축전기의 전기 용량이 커진다.

 

도전율

 

Boundary Conditions

Electric field의 접선 방향의 성분은 서로 같다. 법선 방향 성분은 D1과 D2가 같아지는데 

surface charge가 있으면 그만큼 차이가 난다.

 

도체에서의 Boundary Conditions

 

도체 내부의 전기장은 0이다. why?

접선방향의 경계조건을 구하기 위해서는 폐루프를 한 후에 한바퀴 적분해서 0이된다는것으로부터 접선방향의 곙계조건을 구할 수 있다.

볼륨에 대해서 가우스 법칙을 적용해서 법선방향에 대한 경계조건을 구하고

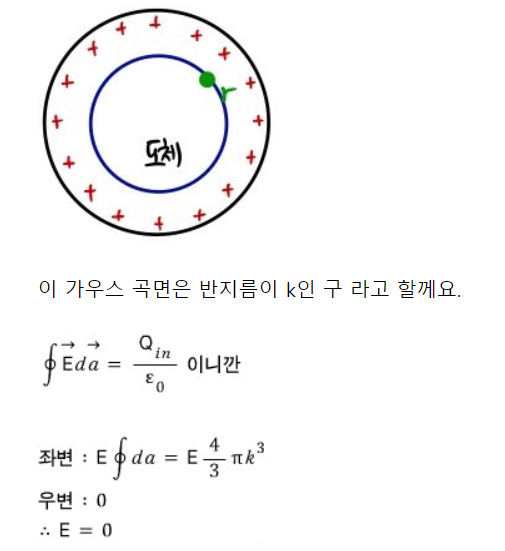
D의 법선방향 성분이 ρs와 같다.

 

Capacitance

도체의 크기 면적, 거리, 형태, 간격등에 의해서 C가 결정이 된다.

Q를 먼저 가정을 해서 가우스 법칙을 적용하기 쉬운 구조면 E를 구한다
곤란한 경우도 있겠지 
여러가지 상황에 따라서 포텐셜을 먼저 가정해야할 경우도 있다

포텐셜을 바운더리에 주게 되면 내부에 포텐셜을 구하고 
V로부터 E를 구하고 D를 구해서 Q를 구할수 있게 된다고 
로우를 구하고 적분해서 Q를 구한다고 

결과적으로 C를 구할 수 있게 되는것이지.

 

포아송 방정식

 

 

Uniqueness theorem for Poisson's equation

From Wikipedia, the free encyclopedia

Jump to navigationJump to search

The uniqueness theorem for Poisson's equation states that, for a large class of boundary conditions, the equation may have many solutions, but the gradient of every solution is the same. In the case of electrostatics, this means that there is a unique electric field derived from a potential function satisfying Poisson's equation under the boundary conditions.

 

Method of images

영상법(映像法, method of images)은 라플라스 방정식의 경계값 문제를 좀 더 쉬운 다른 문제로 바꾸어 푸는 방법이다. 영상법의 타당성은 유일성의 정리에 의해 증명된다. 이 때, 바뀐 문제에서는 원래 문제의 전하에 대응하는 가상의 전하를 추가하므로, 이 가상의 전하를 마치 거울에 비치는 영상에 비유한 것이다.

 

포아송
4장에서는 바운더리 벨류 문제를 푸는데
포아송 방정식이 필요하단 말이지 
포텐셜에대한 포아송 방정식을 구할수있어
가우스 법칙을 사용해서 풀수도 있겠지만 
포아송 방정식의 라플라스를 풀어서 전기장을 구할수있어

유니크니스의 조건은 
어떤 영역안에 솔루션이 유일하게 하기 위한 
경계조건은 DNM 여러가지야 
그러면 유니크하게 결정된다
영상법에대해서 말할수가 있지

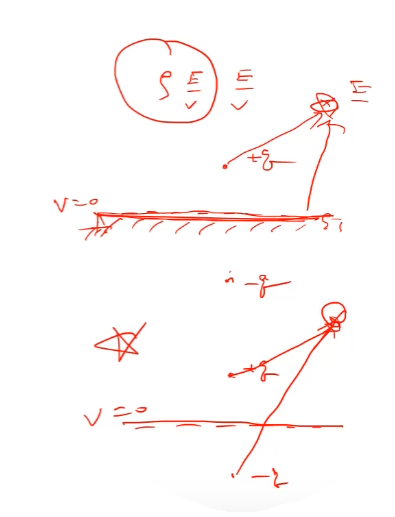
어떤 지점의 E를 구하라 
로우 s로부터 오는 E를 구하기 어렵단말이야
그라운드 되어있으느 V=0 
경계조건으로 uniqueness 이론에 의해서 
바운더리 컨디션이 같으면 솔루션이 유니크하다고 했지
그래서 여기에 마이너스 q를 가정하면 
+q와 -q가 있으면 포텐셜이 0가 되겠지(중간지점이)
+q와 -q에 의해서 발생하는 문제를 푸는게 영상법이야. 

Boundary Value Problems
라플라스식을 만족하고 
경계조건을 주었을 때 V를 주던가 라운드V 라운드n을 주던가 하면 내부에서 문제를 풀수있게되겠죠

그러한 문제를 푸는 몇가지 케이스에 대해서 풀어봤었죠 

전류와 저항등에 관한 이야기를 했었죠

 

Magnetic charge는 존재하지 않는다.

Magnetic의 소스는 발산하는 형태의 자하라는것은 없다고 자하는 없어서 다이버전스 형태는 발생안해 전류로부터 회전하는 형태의 자기장이 발생한다고

 

Ampere's circuital law

어떤 표면에 대해서 적분하면 스톡스의 정리에 의해 선적분으로 바꾸면 앙페르의 주회법칙을 얻는다고 H에 관한 앙패르 법칙을 얻을 수도 있지

 

Vector Magnetic Potential

전류로부터 자기장이 발생하는데 로우로 부터 E를 구했었는데 벡터문제가 되는데 포텐셜을 구해서 E를 구했었잖아 J로부터 B나 H를 구하는데 J와 B는 같은 방향이 아니어서 복잡해 그대서 A를 구해서 B를 구할거야 A는 벡터자기포텐셜이야 J와 A의 방향은 같아 B는 컬A야 이건 B의 다이버전스가 0가 되는것에서 가져온거야 A는 B를 준다고해도 줄수있는 A는 여러가지가 있을수있는데 쿨롬 조건을 사용해서 다이버전스 A는 0이된다고 가정하면 벡터 포아송 equation을 얻게 된다고 J와 A가 같은 방향이라서 세개의 분리된 스칼라 equation으로 볼수가 있어 솔루션이 V는 4파이 입실론제로~~였었지 A에 대한 솔루션도 나오게 되는거야. J로부터 A를 구해서 A로부터 B를 구하는거야

 

비오 사바르의 법칙

비오사바르 법칙 J로부터 바로 B를 구하는 방법이지 Idl이라는 전류가 있으면 거리에 있는 거기서 발생하는 dB 크로스 프로덕트가 된다고 회전하는 방향으로 발생한다는거야 만약에 전류가 미소전류가 아니라 루프로 흐르면 각각의 미소전류로부터 발생하는 자기장을 더해주면 구할수있다. dB내에 또다른 전류소 I2dl2가 들어오면 어떤 힘을 받게 될까? dF12=I2dl2 x dB가 된다구 문제를 풀때 벡터표시는 반드시해줘야돼 Idl1은 dF21을 받겠지 (작용 반작용)

Constitutive Relation 

매질특성 방정식이  B=uH가 될것이야.

In the magnetic material

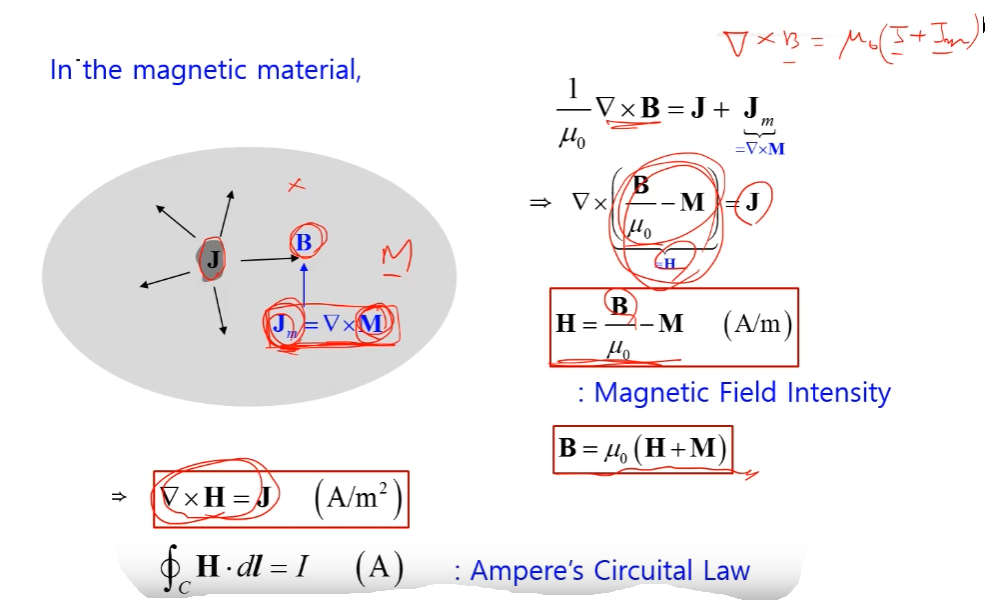
어떤 마그네틱 물질에 자기장을 걸면 
자화 M이 발생한다고 벡터야 이거 
M이 발생하면 등가 전류 자하전류는 
curl M에 해당한다고 
매질 내에서 전류를 흘려주면 자기장이 발생한다고 
자화가 일어나게 되서 전 영역에 걸쳐서 자화가 일어나게 된다고
각 영역에 Jm이 발생해서 
어떤 지점에 발생하는 자기장이 원래 자기장도 있겠지만 
J+Jm이되는거야 
양변에 컬을 몰아서 취하면 위와같이 되고 

컬H는 J가 되는거야 위 관계식으로부터 
magnetic field intensity를 구할수가 있어.

 

Magnetic susceptibility

자화율

자화율이란、자기 분극의 정도를 나타내는 물성값이다. 자기 감수율, 자기화율이라고 하기도 한다.

근데 M이라고 하는것은 자화니까 H에 비례하는데 이걸 서셉트빌러티라고한다고 카이엠이라고 하는것은 어떤 상수를 볼수있겠지만 H값이 커지면 비선형적이게 된다고==>세츄레이션됨 근데 이건 강자성체에서의 이야기야 선형관계에서는 M=XmH가 성립한다고 선형 영역에서 자기장에 대입을하면 1+Xm이 ur이 된다고 대부분 물질은 비자성물질인데 0.99998뭐 이래서 1근방이야 1+Xm이 ==>뮤알을 1로 생각하면된다 근데 강자성체에서는 아니야 6-3을 들어봐