
유한요소법에 대해 설파하기 전에 푸아송 방정식 먼저 풀게 되는데
그전에 가우스 법칙에 대해서 알아보자
Gauss' law


폐곡면(가우스 면)을 임의로 잡았을 때 가우스면을 통과하는 전기선속(F)은 위와 같이 주어진다.
qenc는 가우스면 안(in)에 든 총 전하량이고, ε0는 진공에서의 유전율이다.
유전율이란 무엇인가
유전체의 경우 전류가 직접적으로 흐르지 않고 외부에서 전기장을 걸면 전하가 내부에서 편극되는 현상을 보이는데, 이 편극의 정도가 얼마나 되느냐가 유전율의 척도이며, 그러한 관점에서 부도체를 곧 '유전체'라고 쓰기도 하며, 엡실론(ε)으로 나타낸다.
E 는 전기장이고, da는 가우스면에 수직하고 면적이 da인 면적소 벡터이다.
면적소 벡터의 방향은 어떤 면적소의 영역에 수직하다.
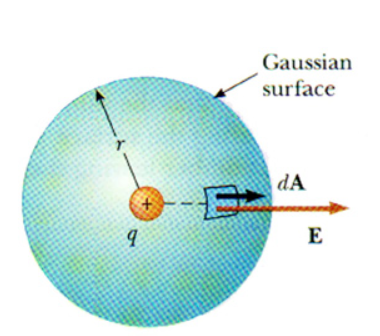
가우스 면을 통과하는 전기선속은 가우스 면 안에 든 전하의 양에 비례한다는 것을 알 수 있다.
어떤 닫힌 공간에 있어서 그 공간의 총 전기선속(electric flux)에 영향을 주는 것은 공간 내부의 전하뿐이라는 것이다.
발산정리를 이용해서 미분형으로 정리할 수 있는데
발산정리(divergence theorem)/가우스 정리

폐곡면 S를 통해 나가는 벡터장 A의 총선속은 A의 발산을 체적적분한 것과 같다.
가우스 법칙에 적용해서 미분형을 유도해보자.






가우스 법칙은 맥스웰의 첫 번째 식이다.
푸아송 방정식
푸아송 방정식은 가우스 법칙의 변형 형태라고 생각하면 쉽다.


'RF 시스템 설계 > 전자기학II' 카테고리의 다른 글
| Boundary Conditions for Magnetostatic Field (0) | 2020.09.07 |
|---|---|
| Poisson's Eq 풀이를 위한 중요 개념 정리 (0) | 2020.09.03 |
| 정전기장 정자기장 복습 [이택경 교수님 강의 6-4,6-3 정리] (0) | 2020.09.03 |
| [전자기학I] 요약 정리 上 (0) | 2020.09.01 |
| [vector][스칼라곱][벡터곱] [coordinate system] (0) | 2020.07.17 |